|
Question 1175277: Practice Age word Problem
Ariana started biking to the library traveling 14 mph, after some time the bike got a flat so Ariana walked the rest of the way, traveling 7 mph. If the total trip to the library took 11 hours and it was 119 miles away, how long did Ariana travel at each speed?
Found 4 solutions by ewatrrr, MathTherapy, ikleyn, greenestamps:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi
D = rt 0r t = D/r
(119-x)/14mph + x/7mph = 11hr
(119-x) +2x = 11hr*14mph
x = 11*14-119 = 35mi which Ariana walked in 5hr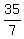 
and 119-35 = 84mi which Ariana biked in 6hr 
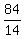Wish You the Best in your Studies.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Practice Age word Problem
Ariana started biking to the library traveling 14 mph, after some time the bike got a flat so Ariana walked the rest of the way, traveling 7 mph. If the total trip to the library took 11 hours and it was 119 miles away, how long did Ariana travel at each speed?
Let the time she spent biking be T
Then time she spent walking = 11 - T
We then get the following DISTANCE equation: 14T + 7(11 - T) = 119
14T + 77 - 7T = 119
14T - 7T = 119 - 77
7T = 42
Time she spent biking, or 
Should now be extremely easy for you to find the time spent walking!
Answer by ikleyn(52799)  (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
You have received two response showing similar formal algebraic solutions.
Here is a very different path to the answer that I personally find much faster and easier (if a formal algebraic solution is not required).
This is essentially a mixture problem -- you are mixing some number of hours at 14mph with some number of hours at 7mph and ending up with a total of 119 miles in 11 hours.
You can solve any two-part mixture problem like that in the following way.
All 11 hours at 7mph would cover 77 miles
All 11 hours at 14mph would cover 154 miles
The actual distance covered was 119 miles
Look at the three mileage totals on a number line; with simple calculations, determine that 119 is 42/77 = 6/11 of the way from 77 to 154.
That means 6/11 of the total time was at the higher rate.
6/11 of 11 hours is 6 hours.
ANSWER: 6 hours at 14mph/ 5 hours at 7mph
CHECK: 6(14)+5(7) = 84+35 = 119
|
|
|
| |
