|
Question 1116921: The perpendicular bisector of the interval CD has equation 4x-3y+16=0. C has coordinates (-9,10). find the coordinates of D
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A PICTURE IS USUALLY HELPFUL:
The line with equation  <--> <-->  has slope has slope  . .
It is easy to see that it passes through point(-4,0).
I can plot points of that line by adding  to the x-coordinate to the x-coordinate
(moving 3 spaces to the right),
and adding  to the y-coordinate to the y-coordinate
(moving 4 spaces up) from any point on the line, including point (-4,0).
That allows me to graph that line, along with point 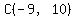 . .

As the line with equation  <--> <-->  and slope and slope  . .
as it is the perpendicular bisector of segment CD,
it is perpendicular to the line CD containing segment CD, and points C and D.
Perpendicular lines have slopes whose product is  , ,
so the slope  of the line containing points C and D is such that of the line containing points C and D is such that
 --> -->  . .
That slope would allow me to plot points of line CD (and graph line CD),
by adding  to the x-coordinate to the x-coordinate
(moving 4 spaces to the right),
and adding  to the y-coordinate to the y-coordinate
(moving 3 spaces down) from any point on the line, including point C(-9,10).
The points added and line CD are shown in green below.
 . .
From point to point on each line, I moved
 units in one direction and units in one direction and  perpendicular to that direction, perpendicular to that direction,
for a distance (along the line) of  , ,
so I see that point C is at a distance  from the blue perpendicular bisector line, from the blue perpendicular bisector line,
so the point at distance  on the other side of that line is point on the other side of that line is point  . .
PROBABLY "FORMULAS" AND EQUATIONS ARE EXPECTED TO BE SHOWN:
The line with equation  <--> <-->  and slope and slope  . .
As it is the perpendicular bisector of segment CD,
it is perpendicular to the line CD containing segment CD, and points C and D.
Perpendicular lines have slopes whose product is  , ,
so the slope  of the line containing points C and D is such that of the line containing points C and D is such that
 --> -->  . .
Knowing the coordinates of 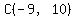 and the slope of the line, and the slope of the line,
we can write the equation of line CD in point-slope form as
 or or  . .
Multiplying both sides of the equal sign times  , and rearranging, we get , and rearranging, we get
 and and  . .
The intersection of linr CD and the perpendicular bisector of segment CD
is the midpoint of CD, and is given by
 . .
Adding up the first equation times 3 plus the second times 4, we get
 --> -->  , ,
and substituting that into  , we get , we get
 --> -->  --> -->  . .
So, the midpoint of CD, 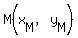 has has  and and  . .
The coordinates of the midpoint of a segment CD, with 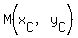 and and 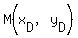 are given by are given by
 and and  . .
Substituting the known coordinates of C and M,
 --> -->  --> --> 
and
 --> -->  --> -->  . .
|
|
|
| |