|
Question 1110617: At the movie theatre, child admission is
$5.20
and adult admission is
$9.10
. On Saturday,
142
tickets were sold for a total sales of
$960.70
. How many child tickets were sold that day?
Found 2 solutions by ikleyn, Boreal:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One line solution
the number of children tickets = 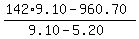 = = 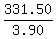 = 85. = 85.
Explanation.
Lets assume for a minute that all sold tickets were adult tickets.
Then the revenue would be 142*9.10 = 1292.20 dollars.
It is 1292.20 - 960.70 = 331.50 dollars more than the actual revenue (! the numerator of my formula !)
The difference is due to the difference between one adult and one children ticket, which is 9.10-5.20 = 3.90 dollars
(! the denominator of my formula !).
So, replacing each adult ticket by one children ticket, we decrease this difference of 222.30 dollars by 3.90 dollars.
By dividing one difference by another, you get the number of children tickets.
Solved.
---------------
You may consider this solution as a joke, but it REALLY WORKS. In reality, IT IS THE ROBUST METHOD of SOLUTION ! !
And if you will get understanding on how and why it works, you will be able to solve ANY of such problems in one line.
================
It is a standard ticket problem.
Read the lessons
- Using systems of equations to solve problems on tickets
- Three methods for solving standard (typical) problems on tickets
in this site. You will find there different methods (actually, ALL applicable methods) for solving such problems.
Learn from these lessons on how to solve such problems once for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! A+C=142
9.1A+5.2C=960.70; multiply top by -5.2 to eliminate C
-5.2A-5.2C=-738.4
3.9A=222.3
A=57
C=85 ANSWER
$518.70 adults
$442 child
Adds to $960.70
|
|
|
| |