SOLUTION: find the maximum value of p=5x+3y under the following constraints:2x+y=<20, 2x+3y=<24, x=>0 and y=>o

1.  Make a plot of the feasible area.
    It is restricted by the straight lines 
    
    2x +  y = 20,     or     y = 20 - 2x;
    2x + 3y = 24,     or     y = ;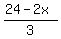
    x = 0                    (y-axis)                and
    y = 0                    (x-axis).

    See the plot below:


              


         Feasibility area. Straight lines 2x + y = 20 (red);  2x + 3y = 24 (green)


    Feasibility area is this quadrilateral in the first quadrant restricted by the straight lines and axes.


2.  The critical points are the vertices of this quadrilateral.

    One vertex is x-intercept of the red line.      It is the point (10,0).

    Second vertex is y-intercept of the green line. It is the point (0,8).

    Third vertex is the intersection point of the red and the green line.
    To find the coordinates of this point, you need to solve the system of two linear equations.
    I did it for you and found the coordinates  (x,y) =             (9,2).


3.  The last step you need to do is to calculate the values of your "profit" function  P(x,y) = 5x + 3y at vertices. You have

    First vertex:   P(10,0) = 5*10 + 3*0 = 50.

    Second vertex:  P(0,8) = 5*0 + 3*8   = 24.

    Third vertex:   P(9,2) = 5*9 + 3*2 = 45 + 6 = 51.


4.  Your "profit" function is maximal at the third vertex.
   
    Then the linear programming method states that it is the solution of your minimax problem.


              The function p(x,y) = 5x + 3y has the maximum value over the feasibility area at the point (x,y) = (9,2), 
              and this maximum value is equal to 51.