Question 1196069: A rectangular box is named ABCDHEFG. Notice that A= (0,0,0) and that B, D, and E are on the coordinate axes. Given that G= (6,3,2), find:
(a) Coordinates of the six other vertices
(b) The lengths AH, AC, AF, and AG
Found 2 solutions by greenestamps, Edwin McCravy:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The description is not sufficient to get a single set of answers to the questions that are asked; the specific answers will be different depending on which of the three coordinate axes the points B, D, and E are located.
With A(0,0,0) and G(6,3,2), the other six vertices, in SOME order, are
(6,0,0), (0,3,0), (0,0,2)
(6,3,0), (6,0,2), (0,3,2)
AH, AC, and AF are diagonals of faces of the box; the lengths will again depend on the locations of B, D, and E.
AG is the space diagonal; its length is 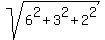 . .
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Greenestamps gave you the coordinates. Here is the 3D graph.
The shortest edges are 2, the medium sized edges are 3, and
the longest edges are 6.
I don't know how your teacher gives the order of the vertices.
I guess B is on the x-axis, D on the y-axis and E is on the z-axis.
So you will have to supply the last 3 letters for the vertices.
G=(6,3,2) is the front upper right vertex
(6,0,2) is the front upper left vertex
B=(6,0,0) is the front lower left vertex
(6,3,0) is the front lower right vertex
(0,3,2) is the back upper right vertex
E=(0,0,2) is the back upper left vertex
A=(0,0,0) is the back lower left vertex
D=(0,3,0) is the back lower right vertex
To find the distances, use
Greenestamps gave you the coordinates. Here is the 3D graph.
The shortest edges are 2, the medium sized edges are 3, and
the longest edges are 6.
I don't know how your teacher gives the order of the vertices.
I guess B is on the x-axis, D on the y-axis and E is on the z-axis.
So you will have to supply the last 3 letters for the vertices.
G=(6,3,2) is the front upper right vertex
(6,0,2) is the front upper left vertex
B=(6,0,0) is the front lower left vertex
(6,3,0) is the front lower right vertex
(0,3,2) is the back upper right vertex
E=(0,0,2) is the back upper left vertex
A=(0,0,0) is the back lower left vertex
D=(0,3,0) is the back lower right vertex
To find the distances, use
  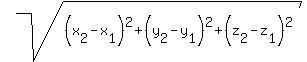 Edwin
Edwin
|
|
|