|
Question 1184227: the center of a circle is at (-3,2) and its radius is 7. Find the length of the chord, which is bisected at (3, 1).
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52787)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
the center of a circle is at ( , , ) => ) => and and 
and its radius is 
equation is:



Find the length of the chord, which is bisected at ( , ,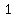 ) )
if the chord is bisected at ( , ,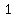 ), find solutions for intersection of the circle with vertical line x=3 ), find solutions for intersection of the circle with vertical line x=3

 is the is the 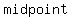 of the chord so angle of the chord so angle 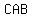 is a is a 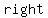 angle. angle.
Use coordinates ( , , ) and ( ) and ( , , ) to find the length of the line segment ) to find the length of the line segment 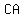 . .
Now you can use Pythagoras theorem to find the length of the line segment  , which is , which is  the length of the chord. the length of the chord.
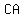 =distance between points ( =distance between points ( , , ) and ( ) and ( , , ) )








 -> half the length of the chord -> half the length of the chord
the length of the chord will be 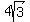 =>answer =>answer
|
|
|
| |