Question 1032601: Im so lost with this worksheet I have to do please help!
It says you and your friend see kids playing on a seesaw. The two kids are balancing without their feet touching the ground. Your friend says there is no way that a mother and daughter could do the same thing. Use what you know about the different types of variation to figure out how a mother and child could balance. The values gave to me are
Weight Distance
120 100
150 80
200 60
300 40
400 30
Write an equation that models your data. Use variables of weight, W, and distance, D. (You will have to use one of your data points to find your constant of variation) Please write the general form of variation and the constant of variation and the final equation.
The second question is The lever tool helps ring values that will balance your seesaw but it has a limited range of precision. Use your graph to estimate a coordinate (W,D) that balances your seesaw. please show correct substitution and verification I really don't get this at all
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website!
W D
120 100
150 80
200 60
300 40
400 30
The graph looks like this, connected with line segments
Note: [I did not mark off the units on the horizontal and
vertical axes, below the points and to the left of the
points, but you should do that on your work-sheet]
Or preferably, connected with a smooth curve, like this
Since the graph goes down as we move to the right, we suspect
that Distance varies INVERSELY as Weight. So we write the
inverse proportional equation
  
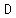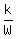We pick any data point to substitute. May as well pick
the W=120 and D=100
 
 
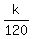
So the equation is
Now plug in your own weight, and find the point that would
balance your seesaw. For instance, if you weigh 130, you
would substitute W = 130, and get
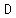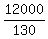
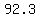 approximately,
which would be your distance, and you would mark your
point, representing your weight and distance,
(W,D) or (130,90.3), say, in red, like this:
Edwin
|
|
|
