Question 870471: Tell whether the ordered pair is a solution of the given system: Show your work PLEASE!
Ordered Pair: (2,-2)
System of Inequalities:
y < x-3
y > -x+3
http://prntscr.com/3ga3w0
copy & paste the link ^^ above to see the ordered pair please, I couldn't write it because it wont let me please help and thank you!
Found 2 solutions by jim_thompson5910, josgarithmetic:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! If the ordered pair, or point, (2,-2) was a solution to the system of inequalities, then it has to make ALL of the inequalities true inequalities (ie true statements).
Something like 1 < 5 is true because 1 is indeed less than 5.
On the other hand, 1 > 5 is false because 1 is smaller than 5 (not the other way around).
To determine if (2,-2) is a solution to the system, we simply plug in (x,y) = (2,-2) into each inequality individually.
Let's plug in (x,y) = (2,-2) into y < x-3
y < x-3
-2 < 2-3 .... plug in (x,y) = (2,-2), ie plug in x = 2, y = -2
-2 < -1
The last inequality -2 < -1 is true since -2 is less than -1.
-------------------------------------------------------
Let's plug in (x,y) = (2,-2) into y > -x+3
y > -x+3
-2 > -(2)+3 .... plug in (x,y) = (2,-2), ie plug in x = 2, y = -2
-2 > -2 + 3
-2 > 1
The last inequality -2 > 1 is false since -2 is really smaller than -1 (not larger).
-------------------------------------------------------
So (x,y) = (2,-2) makes y < x-3 true, but it makes y > -x+3 false.
To be a solution to the system, it has to make ALL of the inequalities of that system true. Because at least one is false (ie not all are true), (x,y) = (2,-2) is NOT a solution to the system.
=================================================================================================
Final Answer: (2,-2) is NOT a solution to the system.
Answer by josgarithmetic(39621)   (Show Source): (Show Source):
You can put this solution on YOUR website! Is the point, (2,-2) a solution to the system:
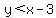
and
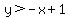
Simply test the point. It either satisfies both inequalities or it does not satisfy both inequalities.
First one:
-2<2-3
-2<-1
YES. True.
Second one:
-2>-(2)+1
-2>-1
NO. False.
That point, (2,-2) is NOT a solution of the system. The point does not satisfy both inequalities.
(The site system has some coding that allows you to write the inequality system the way you want, but that code, I do not immediately know).
|
|
|