|
Question 72917: Suppose a baseball is shot up from the ground straight up with an initial velocity of 64 feet per second. A function can be created by expressing distance above the ground, s, as a function of time, t. This function is s = -16t2 + v0t + s0
•16 represents 1/2g, the gravitational pull due to gravity (measured in feet per second2).
•v0 is the initial velocity (how hard do you throw the object, measured in feet per second).
•s0 is the initial distance above ground (in feet). If you are standing on the ground, then s0 = 0.
a)What is the function that describes this problem?
Answer:
b) The ball will be how high above the ground after 1 second?
Answer:
Show work in this space.
c) How long will it take to hit the ground?
Answer:
Show work in this space.
d) What is the maximum height of the ball? What time will the maximum height be attained?
Answer:
Show work in this space.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Suppose a baseball is shot up from the ground straight up with an initial velocity of
64 feet per second. A function can be created by expressing distance above the ground, s,
as a function of time, t. This function is 
•16 represents 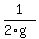 , the gravitational pull due to gravity (measured in feet per second^2). , the gravitational pull due to gravity (measured in feet per second^2).
•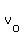 is the initial velocity (how hard do you throw the object, measured in feet per second). is the initial velocity (how hard do you throw the object, measured in feet per second).
•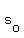 is the initial distance above ground (in feet). If you are standing on the ground, then is the initial distance above ground (in feet). If you are standing on the ground, then  . .
.
a)What is the function that describes this problem?
.
Answer:
.
Start with the equation you are given:
.

.
You are given that the initial velocity is +64 feet per second. Substitute that value for 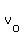
and the equation then becomes:
.

.
Since the baseball is shot up from ground level, you know that the starting height is
zero. Therefore, 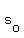 is zero and it just drops from the equation. You are left with: is zero and it just drops from the equation. You are left with:
.

.
and that is the answer to this part of the problem.
.
b) The ball will be how high above the ground after 1 second?
Answer:
.
Show work in this space.
.
In the equation that we got for part a) of this problem, t is in seconds. So all we
have to do is put 1 second into the equation in place of t. If you do that you get:
.

.
This reduces to:
.

.
So the baseball is 48 feet above the ground at 1 second after it is launched.
.
c) How long will it take to hit the ground?
Answer:
.
Show work in this space.
.
There are two times that the ball is at a height of zero feet. The first time is just
at the instant launch begins and the second time is when it hits the ground after it
falls to Earth.
.
Return to the equation we developed as the answer to part a) of this problem.
.

.
Set s equal to zero because we are interested in finding when the baseball is at ground level.
With s set as being equal to zero the equation becomes:
.

.
Factor a t out of the right side of the equation to get:
.

.
Notice that this equation will be true whenever one of the factors on the right side is zero.
When one of these factors is zero, the whole right side multiplies out to be zero and
is then equal to the left side.
.
So this equation is satisfied if either t = 0 or if 
.
Well we knew already that at t = 0 (just at the instant of launch) the ball was at ground
level. So we need to solve the equation for the second factor to find out the second time
that the ball is at ground level. Therefore solve the equation:
.

.
Subtract 64 from both sides to eliminate the 64 on the right side. The equation then becomes:
.

.
If you then divide both sides by -16 the answer for t becomes:
.

.
So the ball is in the air a total of 4 seconds.
.
d) What is the maximum height of the ball? What time will the maximum height be attained?
Answer:
.
Show work in this space.
.
The ball spends half of its flight time going up and the other half of its flight time
falling back to Earth. So it rises for 2 seconds and falls for 2 seconds.
.
Since it rises for 2 seconds you can put 2 seconds into the height equation that we found for
part a) and find the height at that time:
.

.
The ball is at a height of 64 feet at the peak of its flight.
.
I hope this helps you to understand flight concepts. The same basic idea applies to
rocket launches, basketball shots, and football punts and passes.
|
|
|
| |