Question 541311: I have to make a graph of this parabola:
F(x) = x^2 -2x -15
I need the details of how each of the principals points are calculated.
Thank you.
Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website! The easiest point are the intercepts
x-intercept: (x,0)
y-intercept: (0,y)
To find x-intercept(s) ( may be 1 or 2 or none ),
set  ( f(x) is the same as y )
Complete the square by dividing the coefficient
of the x term by 2, square it, and add it to both sides
take the square root of both sides
And, taking the negative root of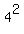 
So, the x-intercepts ( also called roots ) are at
(5,0) and (-3,0)
---------------
To find the y-intercept ( only 1 ), set 
y-intercept = (0, -15)
--------------------
Now you have 3 important points, also since the
coefficient of the  term is positive, the
parabola has a minimum, not a maximum.
The minimum is always exactly between the
x-intercepts, or at ( (5 - 3)/2, y ) = ( 1, y), and to find y,
So, the vertex which is a minimum is at (1, -16)
|
|
|
