|
Question 367062: many elevators have a capacity of 1000 kg.suppose that children(each weighing 35 kg)and adults(each weighing 80 kg) are on elevator.graph a system of linear inequalities that indicates when the elevator is overloaded
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! capacity of an elevator is 1000 kg.
children weigh 35 kg apiece.
adults weigh 80 kg apiece.
x = number of children.
y = number of adults.
your equation for the maximum capacity that the elevator can carry is:
35x + 80y <= 1000
if you solve for y, then you get:
y <= (1000-35x)/80
if x is 0, then you get:
y <= 1000 / 80 which yields:
y <= 12.5
if y is 0, then you get:
0 <= (1000 - 35x) / 80
multiply both sides of this equation by 80 to get:
0 <= 1000 - 35x
add 35x to both sides of this equation to get:
35x <= 1000
divide both sides of this equation by 35 to get:
x <= 28.57142857
your constraints on your equation are that:
x <= 28.57142857
y <= 12.5
you know that the value of x can't be less than 0, so a graph of this equation would have the x value go from 0 to 29.
you know that the value of y can't be less than 0, so a graph of this equation would have the y value go from 0 to 13.
both those extreme value of x and y include the maximum value that x or y can take.
to graph the equation of y <= (1000-35x)/80 by setting the equation to be an equality rather than an inequality to get:
y = (1000-35x)/80
a graph of that equation looks like this:
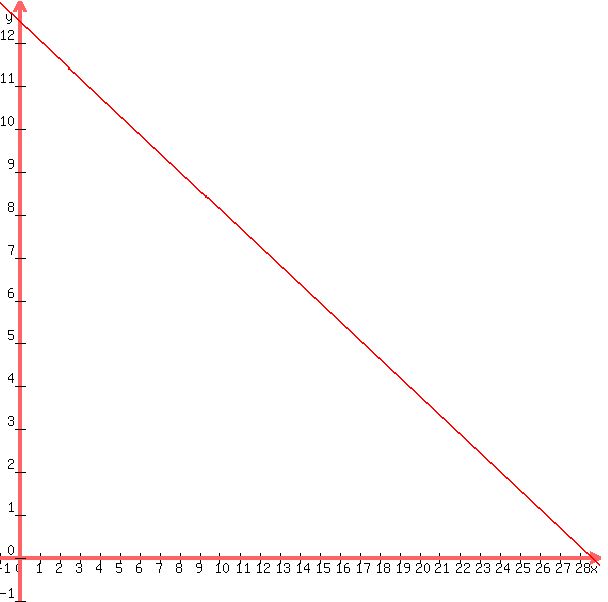
since your equation is really <= the graph of the equation shown, then the values of y can be anything below the graph of the equation.
the values of x will have to be integers (can't have partial children).
the value of y will have to be integers (can't have partial adults).
you will round down to the nearest integer in any situation where the value of x or y is a partial.
any point on the graph of the equation will be the intersection of a horizontal line of the y value and a vertical line of the x value.
suppose you pick x equal to 10.
trace a vertical line on the graph from the x-axis up until it intersects with the graph of the equation.
from that intersection, trace a horizontal line until it intersects with the y-axis.
the intersection point of the horizontal line from the graph of the equation to the y axis will be your y value.
we started with x = 10.
we traced a vertical line up to the graph of the equation of y = (1000-35x)/80, and then we graced a horizontal line from that intersection to the y-axis.
that shows us that when the value of x = 10, the value of y = approximately somewhere around 8.
we don't know exactly, so we'll use the equation to help us.
the equation we use is y = (1000 - 35x) / 80
when x = 10, this equation becomes y = (1000 - 350) / 80
solve for y to get y = 8.125
since this is not an integer, we round down to the nearest integer to get y = 8.
with 8 adults and 10 children, we are within the capacity of the elevator.
8 * 80 + 10 * 35 = 640 + 350 = 990.
we're within the capacity of the elevator and it's clear that we can't add another adult nor can we add another child because doing so will exceed the capacity of the elevator.
likewise, .....
if we pick a value of y = 12, we can look at the graph of the equation and draw a horizontal line from the y-axis until it intersects with the graph of the equation.
from that intersection, we draw a vertical line down until it intersects with the x-axis.
the approximate value of x will be somewhere between 1 and 2 so we can take a good guess at y = 1.
we use the equation of y = (1000 - 35x) / 80 to get the exact value of x.
when y = 12, the equation becomes 12 = (1000 - 35x) / 80.
multiply both sides of this equation by 80 to get:
960 = 1000 - 35x
subtract 960 from both sides of this equation and add 35x to both sides of this equation to get:
35x = 1000 - 960 which simplifies to:
35x = 40
divide both sides of this equation by 35 to get:
x = 1.142857143
round down to the nearest integer to get:
x = 1.
with 12 adults and 1 child, we get a total of 12*80 + 1*35 = 960 + 35 = 995 kg.
we're within the capacity of the elevator and it's clear that we can't add any more adults or children or we'll be above the capacity of the elevator.
as long as we pick a value of x that is to the left of the intersection of the graph of the equation and the x axis, then we can calculate the maximum value of y by looking at the y value of the intersection of the vertical line from that value of x and the graph of the equation.
as long as we pick a value of y that is below the intersection of the graph of the equation and the y-axis, then we can calculate the maximum value of x by looking at the x value of the intersection of the horizontal line from that value of y and the graph of the equation.
any point pair that is within the area bounded by the graph of the equations x = 0, y = 0, and y = (1000-35x)/80 will be within the capacity of the elevator.
any point pair that is outside the area bounded by the graph of the equation x = 0, y = 0, and y = (1000-35x) / 80 will be either outside the capacity of the elevator, or invalid.
any value of x or y smaller than 0 is invalid.
the point pair (x,y) = (29,10) is outside the area and therefore exceeds the capacity of the elevator.
the point pair (x,y) = (4,10) is within the area and therefore is within the capacity of the elevator.
any points that are not clear that they are within the boundaries on the graph should be settled by invoking the equation.
the point pair (x,y) = (4,10) is within the capacity of the elevator because:
10 <= (1000 - 35*4)/80 which simplifies to 10 <= 10.75 which is true.
the point pair (x,y) = (29,10) is outside the capacity of the elevator because:
10 <= (1000 - 35*29) / 80 which simplifies to 10 <= -.1875 which is not true (it is false).
you can see it from the graph or you can see if from the equation.
the area of the graph that is to the right of y = 0 and above x = 0 and beneath y = (1000 - 35x) / 80 is within the capacity of the elevator.
|
|
|
| |