Question 229265: How do you get an equation for a parallel line that passes through a given point?
example: (3,4); y=2x-7
Found 2 solutions by rfer, drj:
Answer by rfer(16322)   (Show Source):
Answer by drj(1380)  (Show Source):
You can put this solution on YOUR website! How do you get an equation for a parallel line that passes through a given point?
example: (3,4); y=2x-7
Step 1. We note that parallel lines have the same slope.
Step 2. The slope-intercept form is given as y=mx+b where m is the slope and b is the y-intercept b at x=0 or point (0,b). Here, the slope of the give line is m=2 since y=2x-7. So now that we have the slope m=2, we need a line that has the same slope passing through (3,4)
Step 3. The slope m is given as
Step 4. Let (x1,y1)=(3,4) or x1=3 and y1=4. Let other point be (x2,y2)=(x,y) or x2=x and y2=y.
Step 5. Now we're given  . Substituting above values and variables in the slope equation m yields the following steps:
Step 6. Multiply (x-3) to both sides to get rid of denominators on both sides of equation.
Step 7. Now add 4to both sides of equation to solve for y.
Step 8. ANSWER: The equation is 
Here's a graph below and note the slope and y-intercept at x=0 or point (0, 2) and the x-intercept at y=0 or at point (51/3, 0)and note it is consistent with the equation when substituting these
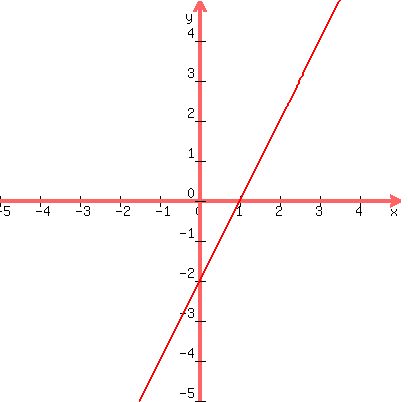
Note: the above equation can be rewritten in standard form as
I hope the above steps were helpful.
For FREE Step-By-Step videos in Introduction to Algebra, please visit http://www.FreedomUniversity.TV/courses/IntroAlgebra and for Trigonometry visit http://www.FreedomUniversity.TV/courses/Trigonometry.
Good luck in your studies!
Respectfully,
Dr J
|
|
|
