|
Question 143034: 3. Given:
a. Find the vertex.
b. Determine whether there is a minimum or maximum value and find that value.
c. Find the range.
d. Find the intervals on which the function is decreasing and the intervals on which the function is increasing.
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! a)
To find the vertex, we first need to find the axis of symmetry (ie the x-coordinate of the vertex)
To find the axis of symmetry, use this formula:
From the equation we can see that a=1 and b=4
 Plug in b=4 and a=1
 Multiply 2 and 1 to get 2
 Reduce
So the axis of symmetry is
So the x-coordinate of the vertex is . Lets plug this into the equation to find the y-coordinate of the vertex.
Lets evaluate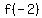 
 Start with the given polynomial
 Plug in
 Raise -2 to the second power to get 4
 Multiply 4 by -2 to get -8
 Now combine like terms
So the vertex is (-2,1)
---------------------------------------------
b)
Since  , this tells us that the parabola is opening upward and that there is a minimum. At the minimum, there is the vertex. So this means that the minimum is  which occurs at
---------------------------------------------
c)
Because the min is , this means that the range is from to infinity. So the range is  which in interval notation is: [ )
---------------------------------------------
d)
At the axis of symmetry, the graph changes from increasing to decreasing (or vice versa). Also, since the graph opens upward, this means that the interval that the function decreases is: ( )
Also, the interval that the function increases is: ( )
Here is the graph of to visually verify our answer
|
|
|
| |
