Question 1203474: Bridge shaped like a parabolic arch has a horizontal distance of 20 feet. The height of a point 1 foot from the center is 8 feet. What is the maximum height of the bridge if it is located at the center?
Found 3 solutions by Edwin McCravy, ikleyn, greenestamps:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Bridge shaped like a parabolic arch has a horizontal distance of 20 feet.
The height of a point 1 foot from the center is 8 feet.
What is the maximum height of the bridge if it is located at the center?
~~~~~~~~~~~~~~~~~~~
Let x-axis be horizontal at the ground level, with the origin under the upper
point of the bridge; y-axis vertical.
Then the parabola has x-intercepts at x= -10 ft and x= 10 ft.
So, the parabola has the form y = a*(x-(-10))*(x-10) = a*(x+10)*(x-10) = a*(x^2-100).
Coefficient "a" is some real negative number (since the parabola is opened downward).
We do not know this number. It is the only unknown in this problem,
and our goal is to find this single unknown.
To find "a", use the fact that at x= 1 ft we have y= 8 ft, from the problem.
It gives you this equation
8 = a*(1^2 - 100), or 8 = -99a, which implies a =  = -0.08080808...
Thus the quadratic function is y = = -0.08080808...
Thus the quadratic function is y =  ,
and it has the maximum at x= 0 (at the axis of symmetry).
Thus the maximum height of the bridge is ,
and it has the maximum at x= 0 (at the axis of symmetry).
Thus the maximum height of the bridge is  = =  = 8.08080808... ft,
or, after rounding, about 8.08 ft. ANSWER = 8.08080808... ft,
or, after rounding, about 8.08 ft. ANSWER
Solved (with the minimum necessary calculations).
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The two responses you have received to this point show variations of a standard formal algebraic solution.
Here is a different, informal method which can sometimes make solving problems like this easier (and sometimes not!)
Since the shape is a parabola, the change in the y value from the axis of symmetry is proportional to the square of the corresponding change in the x value.
The height of the arch is on the axis of symmetry, which we can consider to be x=0.
Let h be the height of the arch -- i.e., the vertex of the parabola is at (0,h). The point (1,8) on the arch is 1 unit horizontally and (h-8) units vertically from the top of the arch; the point (10,0) is 10 units horizontally and h units vertically from the top of the arch.
The second point is 10 times as far from the axis of symmetry as the first, so the difference in the vertical distance from 0 to the top of the arch should be 100 times the difference in the vertical distance from (1,8) to the top of the arch:



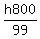 = 8.0808... = 8.0808...
ANSWER: The height of the arch is 8.08 feet, to 2 decimal places.
|
|
|