|
Question 119057: Graph system of Inequality.
2x-y>4
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given to graph:
.
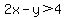
.
One way to work this problem is to recognize that you can manipulate linear inequalities
using the same rules as you do for solving equations, EXCEPT that if you multiply or divide
both sides of an inequality by a negative quantity, you must reverse the direction of the
inequality sign.
.
Knowing this, we can now get the given inequality into a slope-intercept form:
.

.
where m which is the multiplier of x is the slope of the graph, and b, the constant,
is the value on the y-axis where the graph crosses the y-axis.
.
Let's get the inequality into this form. Starting with the given:
.
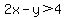
.
Get rid of the 2x on the left side by subtracting 2x from both sides to get:
.
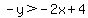
.
Solve for positive y by multiplying both sides of this inequality by -1. Don't forget the
rule that multiplying both sides by MINUS 1 makes it necessary to reverse the direction
of the inequality sign. So multiplying by -1 results in:
.
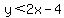
.
If this were an equation, what would the graph of this slope-intercept form look like? It
would have a slope of 2 and it would cross the y-axis at -4. In other words, it would look
like the following graph:
.

.
This graphed line shows all the (x, y) points in which the value of y is EQUAL TO 2x - 4.
.
But in your problem you need to identify all the (x, y) points that have a y-value that
is less than 2x - 4.
.
Those points will be all the (x, y) points that are below the line. [All the points that
have a y value greater than 2x - 4 are ABOVE the graphed line.]
.
So we identify the solution set by shading in the entire area of the graph that is below the
graphed line ... and do not include any points ON the graphed line. You can pick any
(x, y) point in that shaded area and you will find that its y value will be less than you
get if you take its x value and substitute it into 2x - 4.
.
For example, go into the shaded area (that is any place below the graphed line) and pick
any point in that area. Let's take the (x, y) point (+4, -3). If you substitute the value
of x (that is +4) into the function 2x - 4 you get 2(+4) - 4 = 8 - 4 = +4 as the value for
y. But the y value of the selected point is -3, so this selected point has a value of y that is
less than 2x - 4. You can try any number of points in the shaded area. You will get the same
result ... the y value for that point will be less than 2x - 4 where x is the x value of
that point. Therefore, any point in the shaded area satisfies:
.
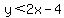
.
which is just a form of the inequality you were given to graph.
.
The graph you are looking for is the shaded area below the graphed line shown in the above graph.
.
Hope this helps you to think your way through the problem so that you understand about graphing
linear inequalities.
.
|
|
|
| |