Question 1168973: (7,7) and (9,2)
I need help finding Leg 1, Leg 2 and the Distance.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Plot the two points on the same xy grid system. Connect them with a line segment. This line segment will be the hypotenuse of the right triangle we'll set up.
To get this right triangle, we'll need a third point (where the 90 degree angle is located). There are two possibilities: We could plot a point at (7,2) or at (9,7)
In this diagram

We have A,B as the two given points (7,7) and (9,2) respectively. The other two points C and D are candidates for the third point to pick.
If you go with point C, then focus on triangle ABC. This is a right triangle with the 90 degree angle at point C.
The distance from A to C is 5 units because point A has y coordinate 7 and point C has y coordinate 2 (which is also the y coordinate of B), so 7-2 = 5 is the length of AC.
Similarly, 9-7 = 2 is the distance from C to B. We subtract the x coordinates to get the horizontal distance.
At this point we know the legs of triangle ABC are 5 and 2. The hypotenuse is unknown but we can use the pythagorean theorem to solve for it.





The distance from point A to B is exactly 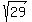 units and approximately units and approximately  units. units.
----------------------------------------------------------------
Another approach is to use the distance formula. This skips the need for a diagram and plotting that third point.
 = (7,7)) is the first point is the first point
 = (9,2)) is the second point is the second point
Plug those coordinate values into the distance formula below. Simplify.




 Exact Distance Exact Distance
 Approximate Distance Approximate Distance
We get the same answer. note the expressions 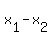 and and 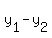 compute the length of the legs of the right triangle as done in the previous section (since we subtracted coordinates to get the horizontal and vertical distances). So basically the distance formula is the pythagorean theorem, but a slightly different version. We've gone from compute the length of the legs of the right triangle as done in the previous section (since we subtracted coordinates to get the horizontal and vertical distances). So basically the distance formula is the pythagorean theorem, but a slightly different version. We've gone from  to to  where c > 0 is the distance we're after, where c > 0 is the distance we're after,  , and , and  . .
|
|
|