Question 1071311: On the graph of an inverse relationship
A. All the points fall in the same quadrant
B. The x-intercept has very large value
C. The x- intercept has a very small value
D. The lines approach, but do not touch the axis.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! When two variables are inversely related to each other,
the relation can be written as
 or  ,
where  is a non-zero constant.
In most examples that constant is positive,
and the graph looks like this
 ,
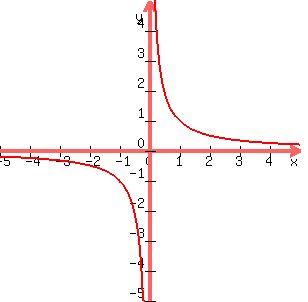or if the relation is only defined for positive values
of  , , and  , it would look like this.
 .
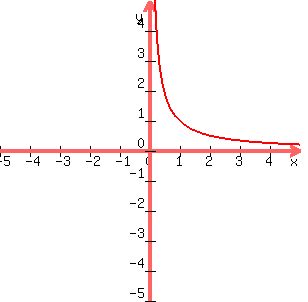If the constant were negative,
the graph would look like this
 .
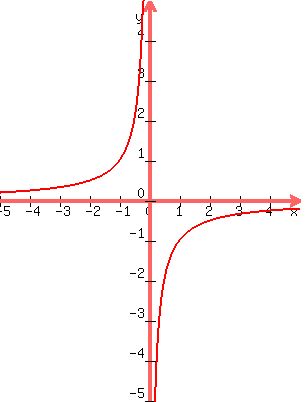A curve like that is called a hyperbola,
and most likely you will meet such curve
and the associated words and equations
at some point in your schooling.
The curve/graph approaches two intersecting lines,
but does not cross them.
When a curve does that
the lines it hugs are called asymptotes.
In the graphs above, the x- and y-axes are the asymptotes.
A Do all the points fall in the same quadrant? For most practical uses,
you start with a positive , have a positive ,
and positive values result. In that case The curve (for only possible x values) stays in the first quadrant.
You cannot find a y value when x=0, but if you choose to define the relation for positive and negative values of x, as the sign of x changes, the graph will jump over the origin to go to another quadrant.
B and C there are no intercepts. The graph does not touch the axes.
D The lines (the graph) approach but do not touch the y-axis. They do not touch the x-axis either.
|
|
|
