Question 659934: a quadrilateral has how many vertices o (0,0) p(3,5) Q(8,6) and R(5,1) determine whether OPQR is a parallelogram
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! vertices O (0,0) P(3,5) Q(8,6) and R(5,1)
determine whether OPQR is a parallelogram
first find the distance between given points:
O (0,0) R(5,1)
P(3,5) Q(8,6)
O (0,0) P(3,5)
R(5,1) Q(8,6)
these are equations of the lines through given points:
 .........O (0,0) R(5,1) .........O (0,0) R(5,1)
 ......P(3,5) Q(8,6) ......P(3,5) Q(8,6)
 ............O (0,0) P(3,5) ............O (0,0) P(3,5)
 .....R(5,1) Q(8,6) .....R(5,1) Q(8,6)

so, OPQR 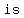 a parallelogram a parallelogram
|
|
|