Question 650170: use slopes to show that the quadrilateral whose vertices are (1.-1), (4,1),(2,2), and (5,4) is a parallelogram
Found 2 solutions by sachi, MathLover1:
Answer by sachi(548)   (Show Source): (Show Source):
You can put this solution on YOUR website! let the vertices of a quadrilateral are A(1.-1), B(4,1),C(2,2), and D(5,4)
then slope AB=[1-(-1)]/[4-1]=2/3
slope CD=[4-2]/[5-2]=2/3
so AB parallel to CD
now
slope AC=[2-(-1)]/[2-1]=3
slope BD=[4-1]/[5-4]=3
so AC parallel to BD
so ABCD is a parallelogram
ans
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! first, a slope for (1.-1), (4,1)
next, a slope for (2,2), and (5,4)
lines have same slope; s0, they are parallel
next, a slope for (1.-1), and (2,2)
and, a slope for (1.-1), and (2,2)
lines have same slope; s0, they are parallel
if both pairs of sides are parallel, then you can conclude that those four points define the  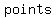 of a of a 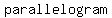

as you can see, their intersection is a 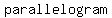
|
|
|