SOLUTION: my teacher gave us an extra credit question which was: given: A=B prove: B=26 he did half of it like this 1. A=b 1. given 2. a*a=b*a 2. multiplication postulate of equali

Algebra ->  Geometry-proofs -> SOLUTION: my teacher gave us an extra credit question which was: given: A=B prove: B=26 he did half of it like this 1. A=b 1. given 2. a*a=b*a 2. multiplication postulate of equali      Log On


   

Question 519318: my teacher gave us an extra credit question which was:
given: A=B
prove: B=26
he did half of it like this
1. A=b 1. given
2. a*a=b*a 2. multiplication postulate of equality
a^2=ba
3. a^2-b^2=ba-b^2 3.multiplication postulate of equality.
(a+b)(a-b)/(a-b)=b(a-b)/(a-b)
4.(a+b)=b
5. b+b=b
the extra credit is to tell him what he did wrong and why?
Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!

Here are all the steps to the bogus proof that 2 = 1.  I put in
a few omitted steps.


1. a = b                 1. given
2. a·a = b·a             2. multiplication postulate of equality
   a² =  ba
3. a²-b² = ba-b²         3.multiplication postulate of equality.

3A. (a-b)(a+b) = b(a-b)  3A. Factoring both sides

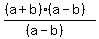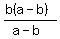3B. %28%28a%2Bb%29%28a-b%29%29%2F%28%28a-b%29%29 = %28b%28a-b%29%29%2F%28a-b%29    3B. Division postulate

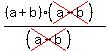3C. %28%28a%2Bb%29%28cross%28a-b%29%29%29%2F%28%28cross%28a-b%29%29%29 = %28b%28cross%28a-b%29%29%29%2F%28cross%28a-b%29%29  3C. Cancelling
  
4.  a+b = b              4.  What you get when you divide.   
5.  b+b = b              5.  Substitution postulate using 1, a=b
     2b = b              
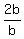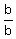6.  2b%2Fb = b%2Fb               6. Division postulate of equality.
7.   2 = 1               7.  Wow!!!

The fallacy is in 3B, the division postulate of equality states that
"If equal quantities are divided by equal nonzero quantities,
 the quotients are equal".  The key word here is NONZERO.  We must always
be sure that we are not dividing equal quantities by 0.  Here 0 is 
camouflaged as (a-b).  Step 1 stated that a=b, and that means that a-b=0.
So when we divided by (a-b) in step 3B, we were dividing by zero, which is 
not defined in mathematics.

Edwin