Question 405635: Prove that if an equilateral triangle is constructed on each side of a given triangle and the third vertex of each of these triangles is joined to the opposite vertex of the original triangle, then the three segments determined are congruent.
Answer by richard1234(7193)   (Show Source): (Show Source):
You can put this solution on YOUR website! Our diagram looks something like this:

(It may appear that these three lines intersect at a point, but that might not necessarily be the case!)
This may seem like an unusual solution, but I believe it is by far the easiest method, and more efficient than trying to brute-force the problem. I will begin by introducing complex numbers into the problem. We can assume that points A, B, ..., F are points on the complex plane.
Suppose that A is the origin of the complex plane, i.e. A = 0, and that B and C are arbitrary complex numbers. It follows that:
 and and  where where  (The Greek letter "omega" denotes a root of unity, in this case, a 6th root of unity. These equations basically state that F is equal to point C rotated about (The Greek letter "omega" denotes a root of unity, in this case, a 6th root of unity. These equations basically state that F is equal to point C rotated about  , and B is the same as D rotated about , and B is the same as D rotated about  .) We want to show that CD and BF have equal magnitudes. Since CD = D - C and BF = F - B (this is similar to subtracting vectors), then we want to show that .) We want to show that CD and BF have equal magnitudes. Since CD = D - C and BF = F - B (this is similar to subtracting vectors), then we want to show that
|D - C| = |F - B| where |z| denotes the magnitude of the complex number z.
Note that  and and  . We can substitute these into our equation to obtain . We can substitute these into our equation to obtain
|D - C| = |(C - D)*omega|. Here, we note that the magnitude of D-C is the same as C-D (i.e. a complex number in the form a+bi has the same magnitude as the number -a-bi). Also, the magnitude of 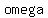 is equal to is equal to  which is 1. Hence, the magnitude remains unchanged, and we conclude that |D - C| = |F - B| and that CD = BF. By a simple symmetry argument (e.g. assigning B as the origin to show that BF = AE), we conclude that CD = BF = AE, and we are done. which is 1. Hence, the magnitude remains unchanged, and we conclude that |D - C| = |F - B| and that CD = BF. By a simple symmetry argument (e.g. assigning B as the origin to show that BF = AE), we conclude that CD = BF = AE, and we are done.
|
|
|