SOLUTION: Given points A(0,0) B(4,8) and C(6,2) are the vertices of triangle ABC. A. Show that triangle ABC is an isosceles triangle B. Find the coordinates of D , the midpoint of the base

Algebra ->  Geometry-proofs -> SOLUTION: Given points A(0,0) B(4,8) and C(6,2) are the vertices of triangle ABC. A. Show that triangle ABC is an isosceles triangle B. Find the coordinates of D , the midpoint of the base      Log On


   

Question 397932: Given points A(0,0) B(4,8) and C(6,2) are the vertices of triangle ABC.
A. Show that triangle ABC is an isosceles triangle
B. Find the coordinates of D , the midpoint of the base.
C. Show that CD is perpendicular to AB
Found 2 solutions by ewatrrr, MathLover1:
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!


Hi

 

A. Show that triangle ABC is an isosceles triangle

B(4,8) and C(6,2)                       A(0,0) and C(6,2)

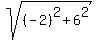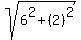
distance AB = sqrt%28+%28-2%29%5E2+%2B+6%5E2%29= distance AC = sqrt%286%5E2+%2B%282%29%5E2+%29



B. Find the coordinates of D , the midpoint of the base AB

A(0,0) and B(4,8)

Midpoint(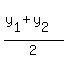%28x%5B1%5D+%2B+x%5B2%5D%29%2F2, %28y%5B1%5D+%2B+y%5B2%5D%29%2F2) (4/2,8/2) OR PT(2,4)



C. Show that CD is perpendicular to AB

 m of CD = %284-2%29+%2F%28+2-6%29+=+2%2F-4+=+-1%2F2

 m of AB = 8/4 = 2

 SLOPES negative reciprocals, lines perpendicular

Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

Given points A(0,0), B(4,8) and C(6,2) are the vertices of triangle ABC
a) Use the distance formula to compute the lengths of sides AB,
BC, and AC. If two of those lengths are equal, the triangle
is+isosceles.

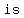A(0,0), B(4,8)...... side AB

Solved by pluggable solver: Distance Formula to determine length on coordinate plane
The distance (d) between two points is given by the following formula:

d=sqrt%28%28x2-x1%29%5E2+%2B+%28y2-y1%29%5E2%29

Thus in our case, the required distance is
d=sqrt%28%284-0%29%5E2+%2B+%288-0%29%5E2%29=+8.94427190999916+


For more on this concept, refer to Distance formula.




B(4,8) and C(6,2).........side BC

Solved by pluggable solver: Distance Formula to determine length on coordinate plane
The distance (d) between two points is given by the following formula:

d=sqrt%28%28x2-x1%29%5E2+%2B+%28y2-y1%29%5E2%29

Thus in our case, the required distance is
d=sqrt%28%286-4%29%5E2+%2B+%282-8%29%5E2%29=+6.32455532033676+


For more on this concept, refer to Distance formula.



AC

A(0,0) and C(6,2).........side AC

Solved by pluggable solver: Distance Formula to determine length on coordinate plane
The distance (d) between two points is given by the following formula:

d=sqrt%28%28x2-x1%29%5E2+%2B+%28y2-y1%29%5E2%29

Thus in our case, the required distance is
d=sqrt%28%286-0%29%5E2+%2B+%282-0%29%5E2%29=+6.32455532033676+


For more on this concept, refer to Distance formula.



AC=6.32455532033676


so, AB+=+8.94427190999916 is NOT equalBC=6.32455532033676,
but, BC=6.32455532033676 and AC=6.32455532033676 are equal in
length , and the triangle 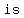is +isosceles

b) Use the 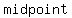midpoint formula with the endpoints of the base of the
triangle. (The side whose length is not equal to that of either of the other
two sides is the base of triangle ABC.)

AB+=+8.94427190999916 is the base of the triangle

Solved by pluggable solver: Find the Midpoint
Let C=the midpoint
x-coordinate+of+C=%28%28x-coordinate+of+A%29%2B%28x-coordinate+of+B%29%29%2F%282%29
x-coordinate+of+C=%280+%2B+4%29%2F%282%29
x-coordinate+of+C=4%2F2
x-coordinate+of+C=2
y-coordinate+of+C=%28%28y-coordinate+of+A%29%2B%28y-coordinate+of+B%29%29%2F%282%29
y-coordinate+of+C=%280+%2B+8%29%2F%282%29
y-coordinate+of+C=8%2F2
y-coordinate+of+C=4
Therefore,
The midpoint C is located at (2,4)



midpointD is at (2,4)

c) Compute the 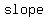slope of CD and of AB. There is a relationship
between the slopes of perpendicular lines; do the slopes of CD and
AB satisfy that relationship?


the 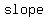slope of CD


Solved by pluggable solver: Finding the slope


Slope of the line through the points (6, 2) and (2, 4)



m+=+%28y%5B2%5D+-+y%5B1%5D%29%2F%28x%5B2%5D+-+x%5B1%5D%29


m+=+%284+-+2%29%2F%282+-+6%29


m+=+%282%29%2F%28-4%29


m+=+-1%2F2



Answer: Slope is m+=+-1%2F2




the slope is m=-%281%2F2%29


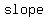the slope of AB

Solved by pluggable solver: Finding the slope


Slope of the line through the points (0, 0) and (4, 8)



Answer: Slope is m+=+2



m=2
since the slope of CD is m=-%281%2F2%29 and the slope of AB is the slope
is m=2, they satisfy a relationship between the slopes of perpendicular lines