Question 1152198: Let ABCD be an isosceles trapezoid, with bases AB and CD. A circle is inscribed in the trapezoid. (In other words, the circle is tangent to all the sides of the trapezoid.) The length of short base AB is 2x, and the length of long base CD is 2y. Prove that the radius of the inscribed circle is sqrt(xy).
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let ABCD be an isosceles trapezoid, with bases AB and CD. A circle is inscribed in the trapezoid.
(In other words, the circle is tangent to all the sides of the trapezoid.)
The length of short base AB is 2x, and the length of long base CD is 2y.
Prove that the radius of the inscribed circle is sqrt(xy).
~~~~~~~~~~~~~~~~~~
Solution
First, make a sketch of the trapezoid and the inscribed circle.
Let AB be the long base of the trapezoid, |AB| = 2y, and let CD be the short base, |CD| = 2x.
Let O be the center of the inscibed circle.
Draw the perpendicular from the point O to the base AB, and let the point E be the foot of this perpendicular
at the base AB (the intersection point). Obviously, |AE| = y.
Draw the perpendicular from the point O to the lateral side AD, and let the point F be the foot of this perpendicular
at the side AD (the intersection point, which is the tangent point, too).
Obviously, |AF| = y. (Since the triangles AOE and AOF are congruent).
Similarly, the length of the segment DF is equal to x: |DF| = x.
Thus the length of the lateral side AD of the trapezoid ABCD is equal to (x+y): |AD| = x + y.
Draw the perpendicular from the vertex D to the base AB. Let J be the foot of this perpendicular at the base AB.
Consider the triangle ADJ.
It is right angled triangle.
Its hypotenuze AD has the length (x+y).
Its leg DJ has the length of (2r), where r is the radius of the inscribed circle.
Its other leg AJ has the length of 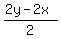 = y - x units.
Write the Pythagorean identity = y - x units.
Write the Pythagorean identity
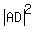 = = 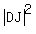 + + 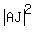 , or , or
 = = 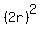 + + 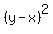 .
Simplify it .
Simplify it
 = = 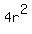 + + 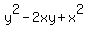 2xy =
2xy = 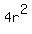 - 2xy
4xy = - 2xy
4xy = 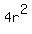 xy =
xy =  r =
r =  .
It is exactly what has to be proved. .
It is exactly what has to be proved.
The solution is completed.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let E and F be the midpoints of bases AB and CD respectively. Then AE=x and DF=y; and segment EF is a diameter of the inscribed circle, so its length is 2r, where r is the radius of the inscribed circle.
Let H be on DF such that AH is perpendicular to DF; then the length of AH is also 2r.
Let G be the point of tangency of the inscribed circle with side AD of the trapezoid.
By the theorem about the lengths of tangents to a circle, AG=AE=x and DG=DF=y.
Finally, the length of DH is y-x.
Now look at right triangle ADH. It has legs of length (y-x) and 2r and hypotenuse of length (x+y).
Use of the Pythagorean Theorem with those lengths will lead you to the desired result.
I leave the calculations to you....
|
|
|