Question 1075229: Please help me with the following proof. Thank you!
How to prove statement "If a rectangle is a square, then its diagonals are perpendicular" and its converse " If the diagonals of a rectangle are perpendicular, then the rectangle is a square"
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If a rectangle is a square,
then all its 4 sides are congruent.
Each of its diagonals splits the square into
two isosceles right triangles.
Each one is a right triangle,
because it has a right angle from the rectangle/square,
and it is isosceles because it has two congruent legs
(that are two congruent adjacent sides of the square).
Then, each of those isosceles right triangles has two 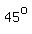 base angles. base angles.
Those are the angles between the diagonals and the sides of the square.
together, the two diagonals split the square into four triangles.
Each of those four triangles has two 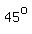 angles, angles,
adjacent to the side that is a side of the square.
The remaining angle, the one between the two sides along diagonals of the square,
must be a  angle, angle,
so the diagonals are perpendicular.
If the diagonals of a rectangle are perpendicular,
then they split the rectangle into 4 right triangles.
The diagonals of a parallelogram (including a rectangle) bisect each other.
If we call the diagonals' lengths 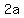 and and 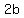 , ,
we can say that each of those 4 right triangles has,
one leg of length  and one leg of length and one leg of length  . .
Those 4 right triangles must be congruent,
meaning that their hypotenuses must be congruent,
and since those hypotenuses are sides of the rectangle,
the rectangle has 4 congruent sides,
which makes it a square.
|
|
|