Question 1017072: If a, b, c are odd integers, then the equation  has no FRACTION solution.
I know how to prove, if it said integer solution, but to prove that theres no fraction solution, it seems a little hard for me.
Im really sorry if its the wrong section
Thanks~!
Found 2 solutions by ikleyn, richard1234:
Answer by ikleyn(52798)   (Show Source):
You can put this solution on YOUR website! .
If a, b, c are odd integers, then the equation has no FRACTION solution.
I know how to prove, if it said integer solution, but to prove that theres no fraction solution, it seems a little hard for me.
Im really sorry if its the wrong section
Thanks~!
--------------------------------------
Assume the equation  =  with odd integer coefficients a, b an c has the solution,
which is a rational fraction  with integer p and q.
We can assume that all the common divisors of p and q are just canceled in the fraction ,
so that p and q are relatively primes integer numbers. In particular, p and q are not both multiples of 2 simultaneously.
Then substitute the fraction into the equation.
You will get  = .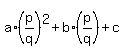
Multiply both sides by  to rid off the denominators. You will get
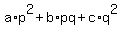 = . (1)
Now, if p is odd, then q can not be multiple of 2, otherwise you easily get a contradiction due to equation (1).
Similarly, if q is odd, then p can not be multiple of 2, otherwise you easily get a contradiction due to equation (1).
Thus both p and q must be odd.
Then the equation (1) has three odd addends that sum up to zero, which is impossible.
This contradiction completes the proof.
Answer by richard1234(7193)  (Show Source):
You can put this solution on YOUR website! You probably mean *rational* solution (since "fraction" is somewhat ambiguous).
The roots of the equation are  . It suffices to prove that  cannot be a perfect square, otherwise the solutions would be rational.
If is a perfect square, then  where a, b, c are odd integers and n is an integer. Note that n is odd, since b^2 is odd and 4ac is even.
Here, we use a little modular arithmetic. The right hand side must leave a remainder of 4 when divided by 8, since a and c are odd. However, all of the odd squares leave a remainder of 1 when divided by 8, meaning that their difference is a multiple of 8. Since the remainders upon division by 8 are not equal, the expressions  and  cannot possibly be equal, and there is no solution in odd integers a,b,c. Therefore cannot be a perfect square, no rational solution.
In modular arithmetic terms, we say that  and  .
|
|
|
