Question 995547: a trapezoidal gutter is to be made, from a strip of metal 12m wide by bending up the edges. Determine where to bend the metal and the angle to bend it at to maximise the cross sectional area and hence the capacity of the gutter
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The fact that the problem asks about "the angle" to bend the metal,
means that the trapezoid section is an isosceles trapezoid,
with the same angle on either side of each base.
 with 
The area is a function of  and  .
Because of its definition as  ,  ,
but  would give us a zero area,
and we know that for  ,  would give us a larger area,
so we expect that for maximum area we need  .
Also, we know that  ,
and since  would give us a zero area,
we expect that for maximum area we need  .
We need to find a maximum for the function
in the domain  .
Towards the boundaries and ,  tends to zero.
On each of the boundaries  and  ,
is a function of the other variable,
with a maximum of  .
Is there a local maximum, with 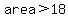 somewhere in the middle of the domain?
If there is one, the partial derivatives at that point are zero.
 --->
 --->
So we have to solve
---> ---> --->
Substituting 0 into we get
 ---> ---> ---> --->  ---> or  .
Then  ---> .
So bending lengthwise the 12m wide strip of metal at  angles along two lines  from the edges, you get a gutter with a section in the shape of an isosceles trapezoid with maximum area.
That maximum area is
 
|
|
|
