Question 412212: 4 congruent circles, each of which is tangent externally to 2 of the other circles, are circumscribed by a square of area 16. A small circle is then placed in the center so that it is tangent to each of the four circles. Determine the radius of the smallest circle.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 Since the area of the square is 16 square units, each side of the
square is the square root of 16 or 4 units.
This green line:
Since the area of the square is 16 square units, each side of the
square is the square root of 16 or 4 units.
This green line:
 is also 4 units and goes across both circles on the left.
so each of the four larger circles has radius 1.
Now let's draw a diagonal of the square and letter some points:
is also 4 units and goes across both circles on the left.
so each of the four larger circles has radius 1.
Now let's draw a diagonal of the square and letter some points:
 ABC is a right triangle,
AB=1, BC=1, so by the Pythagorean theorem AC =
ABC is a right triangle,
AB=1, BC=1, so by the Pythagorean theorem AC =  and since GH = AC, GH =
and since GH = AC, GH =  CD and FG are both radii of the larger circles so they are 1 each.
Triangle AIH is a right triangle, AI = 4, IH = 4, so by the
Pythagorean theorem, diagonal AH =
CD and FG are both radii of the larger circles so they are 1 each.
Triangle AIH is a right triangle, AI = 4, IH = 4, so by the
Pythagorean theorem, diagonal AH =  We add up the parts of the diagonal AH and equate the sum to
We add up the parts of the diagonal AH and equate the sum to  AC + CD + DF + FG + GH =
AC + CD + DF + FG + GH =  Substituting the values for the parts that we know the lengths of:
Substituting the values for the parts that we know the lengths of:
 +1+DF+1+ +1+DF+1+ = =  Now we solve for DF
Now we solve for DF
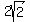 +2+DF = +2+DF =  DF =
DF = 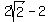 DF is the diameter of small circle E, so its radius
is
DF is the diameter of small circle E, so its radius
is 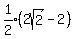 or or
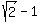 Edwin
Edwin
|
|
|