SOLUTION: Find all points having a y-coordinate of -6 whose distance from the point (1,2) is 17. (a)By using the Pythagorean Theorem. (b)By using the distance formula.

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: Find all points having a y-coordinate of -6 whose distance from the point (1,2) is 17. (a)By using the Pythagorean Theorem. (b)By using the distance formula.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1209063: Find all points having a y-coordinate of -6 whose distance from the point (1,2) is 17.
(a)By using the Pythagorean Theorem.
(b)By using the distance formula.
Found 2 solutions by mccravyedwin, ikleyn:
Answer by mccravyedwin(406) About Me  (Show Source):
You can put this solution on YOUR website!

The green line is the set of all points having a y-coordinate of 6.
The green circle, with center (1,2) and radius 17, is the set of all points
whose distance from point (1,2) is 17.  So the 2 points they have in common
are the only two points having both properties.  So the answer will be those
two points.

B is 6 units above the x-axis and A is 2 units above the x-axis, so the
distance AB = 6-2 = 4.

We have AB=4 and AC=17, BC=sqrt%28AC%5E2-AB%5E2%29=sqrt%2817%5E2-4%5E2%29=sqrt%28289-16%29=sqrt%28273%29.

B is 1 unit farther to the right of the y-axis, so is C, and therefore

C=%28matrix%281%2C3%2C1%2Bsqrt%28273%29%2C%22%2C%22%2C6%29%29

That makes C' one unit less to the left of the y-axis, so

%22C%27%22=%28matrix%281%2C3%2C1-sqrt%28273%29%2C%22%2C%22%2C6%29%29 



--------------

Distance formula:

Let the point (x,y) [where y=6, which means the point (x,6)] have distance
17 from point (1,2).

Then 

d=sqrt%28%28x-1%29%5E2%2B%286-2%29%5E2%29
17=sqrt%28x-1%29%5E2%2B4%5E2%29
17=sqrt%28%28x-1%29%5E2%2B16%29
17=sqrt%28%28x-1%29%5E2%2B16%29
Square both sides:
289=%28x-1%29%5E2%2B16
273=%28x-1%29%5E2
%22%22+%2B-+sqrt%28273%29=x-1
1+%2B-+sqrt%28273%29=x

Thus the two points are 

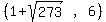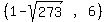%28matrix%281%2C3%2C1%2Bsqrt%28273%29%2C%22%2C%22%2C6%29%29 and %28matrix%281%2C3%2C1-sqrt%28273%29%2C%22%2C%22%2C6%29%29

Edwin

Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.
Find all points having a y-coordinate of -6 whose distance from the point (1,2) is 17.
(a)By using the Pythagorean Theorem.
(b)By using the distance formula.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


        In the post by  Edwin,  the solution and the answer are incorrect.
        In his solution,  Edwin mistakenly used  y-coordinate  6  instead of the given  -6.
        His plot is inadequate,  too.

        I came to bring a correct solution. 


Let's call the given point A = (1,2).


All points having y-coordinate of -6, lie on the horizontal line y = -6.

Vertical distance from the point (1,2) to this line (or simply the distance) is 6+2 = 8 units.

This distance is the length of the perpendicular from this point (1,2) to the line y= -6.


We want to find points C on the line y= -6 such that the distance from A to C is 17 units.


Draw the perpendicular AB from A to line y= -6.  The length of this perpendicular is 8 units.  
The coordinates of B are (1,-6).


The triangle ABC is a right-angled triangle.


Its diagonal AC has the length of 17 units;  its leg AB is of 8 units.


Hence, the leg BC along the line y = -6 is  (Pythagoras)


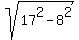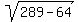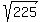    sqrt%2817%5E2+-8%5E2%29 = sqrt%28289-64%29 = sqrt%28225%29 = 15 units.


Thus possible points C are  (1+15,-6) = (16,-6)  or  (1-15,-6) = (-14,-6).


ANSWER.  There are two such points  C = (16,-6)  and  C' = (-14,-6).

Solved  (correctly).