Question 1209028: If two vertices of an equilateral triangle are (0,0) and (0,4), find the third vertex. How many of these triangles are possible?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
The side connecting points A = (0,0) and B = (0,4) is vertical y-axis.
The third vertex C lies on the perpendicular to AB in its midpoint.
The midpoint of AB is the point (0,2).
The perpendicular to AB in its midpoint is horizontal line y= 2.
The altitude of this equilateral triangle has the length  =  =  .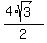
This altitude is the distance of the third vertex C from y-axis - hence, it gives x-coordinate of vertex C.
Thus, the point C, which is the third vertex of the triangle, has coordinates (x,y) = (+/-, ).
So, one version is when triangle ABC lies in the first quadrant. Then its third vertex is (x,y) = (,).
Another version is when triangle ABC lies in the second quadrant. Then its third vertex is (x,y) = ( ,).
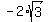So, there are two possible equilateral triangles ABC and two different positions for vertex C.
Solved.
All you need to know and to use to solve this problem is basic elementary properties of equilateral triangles.
By knowing it and using it, you solve this problem MENTALLY in 10 or 20 seconds.
|
|
|
