Question 1195057: Graph a triangle ABC and perform a translation of (x + 4, y − 3) to create triangle A′B′C′.
Describe the transformation using words. Make sure you refer to the characteristics and the coordinates.
Draw a line through points A and A′ and through points B and B′. What do you notice about the lines you drew? Do you think you would notice the same characteristics if you drew another line through points C and C′? How do you know?
Found 2 solutions by MathLover1, Edwin McCravy:
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website! Try drawing the triangle with a vertex at ( , ), another at (,  ), and the last at ( , ).
Transform by changing the coordinates ( ,  ):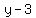
so the (, ) becomes A'=(, ),
the (, ) becomes B'=(, ), and
the (, ) becomes C'=( ,)
Answer by Edwin McCravy(20055)  (Show Source):
You can put this solution on YOUR website!
She didn't answer your questions, but just drew the triangles, but
didn't draw the line segments AA', BB', and CC'. But then, the lines
would have been cluttered and hard to see.
Here is her second drawing, cropped,
Now I'll draw in the line segments AA', BB', CC' in red.
If you'll look carefully, you'll see they all look both parallel and
equal in length.
Let A = (p,q), B = (r,s), and C = (t,u).
She picked p=0, q=0, r=0, s=4, t=5, u=0, but you can pick ANY numbers you
like for them as long as they're different points:
A = (p,q), so A' = (p+4, q-3)
B = (r,s), so A' = (r+4, s-3)
C = (t,u), so A' = (t+4, u-3)
     
  
  
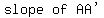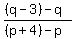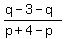
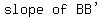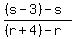
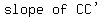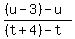They all have the same slope, -3/4, which means that the three lines will be
parallel, regardless of what you choose for points (p,q), (r,s), and (t,u).
Not only that, but what about their lengths?
     
  
  
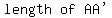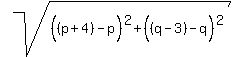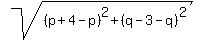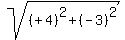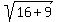
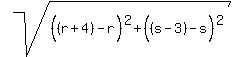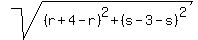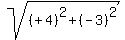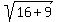
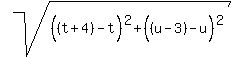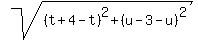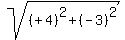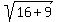The lengths of those parallel lines are also the same, 5.
The two triangles ABC and A'B'C' are also necessarily congruent, right? Or
wrong?
Edwin
|
|
|
