Question 1171703: A Norman window consists of rectangle surmounted by a semicircle. If the
perimeter of a Norman window is 32 ft, what should be the radius of the
semicircle and the height of the rectangle such that the window will admit most
light?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52782)   (Show Source): (Show Source):
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let x = the radius of the semicircle, which is half the base of the rectangle.
Let h = the height of the rectangle.
This drawing is not to scale:
 The area of the semicircle is half the area of a whole circle.
The area of a whole circle circle is
The area of the semicircle is half the area of a whole circle.
The area of a whole circle circle is
 so the area of the semicircle on top is
so the area of the semicircle on top is 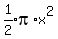 The area of the rectangle is
The area of the rectangle is  So what we want to maximize is the total area y:
So what we want to maximize is the total area y:
 The perimeter of the entire window is given as 32 feet.
The perimeter ("circumference") of the semicircle is half the perimeter ("circumference") of a whole circle.
The perimeter "circumference" of a whole circle is
The perimeter of the entire window is given as 32 feet.
The perimeter ("circumference") of the semicircle is half the perimeter ("circumference") of a whole circle.
The perimeter "circumference" of a whole circle is
 so the perimeter ("circumference") of the semicircle on top is
so the perimeter ("circumference") of the semicircle on top is 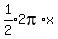 or or 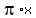 The total perimeter is the perimeter of the semicircle plus the left, right,
and bottom sides of the rectangle.
The total perimeter is the perimeter of the semicircle plus the left, right,
and bottom sides of the rectangle.
 And since the perimeter is 32 feet,
And since the perimeter is 32 feet,

 Substituting for 2h in the equation for the area:
Substituting for 2h in the equation for the area:






 From this point you can get the maximum value by just algebra,
using the vertex formula, or by using calculus. Ikleyn used
calculus above so I'll just use algebra.
The x-coordinate of the vertex of a parabola is
From this point you can get the maximum value by just algebra,
using the vertex formula, or by using calculus. Ikleyn used
calculus above so I'll just use algebra.
The x-coordinate of the vertex of a parabola is  , where 'a' is the
coefficient of x2, and 'b' is the coefficient of x. , where 'a' is the
coefficient of x2, and 'b' is the coefficient of x.
 So the x coordinate when the area is a maximum is
So the x coordinate when the area is a maximum is
 , which is the radius of the semicircle.
Finally we find the height of the rectangle, by substituting , which is the radius of the semicircle.
Finally we find the height of the rectangle, by substituting
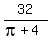 for x in: for x in:


 Divide every term by 2
Divide every term by 2







 The radius of the semicircle equals the height. So the rectangle is twice as
wide as it is high. So it looks like this:
The radius of the semicircle equals the height. So the rectangle is twice as
wide as it is high. So it looks like this:
 Edwin
Edwin
|
|
|