SOLUTION: The midline of a trapezoid is not concurrent with the diagonals. Explain why.

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: The midline of a trapezoid is not concurrent with the diagonals. Explain why.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1156832: The midline of a trapezoid is not concurrent with the diagonals. Explain why.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The midline passes through the trapezoid parallel to both bases.

Each diagonal passes through the trapezoid from a point on one base to a point on the other base.

So each diagonal intersects the midline; that means neither of them is concurrent with the midline.

Answer by ikleyn(52799) About Me  (Show Source):
You can put this solution on YOUR website!
.

            Tutor @greenestamps incorrectly interprets the notion of concurrency for straight lines.

            Therefore, his solution is incorrect.

            I came to bring the correct solution. 


Let me start reminding you two facts from Geometry.


   1)  A trapezoid is a quadrilateral, which has two opposite sides PARALLEL and IS NOT a parallelogram, at the same time.

   2)  Three lines in a plane are called concurrent if they intersect in one common point.


So, the question is to explain why two diagonals of the trapezoid and its midline DO NOT intersect in one common point.


I will try to make my explanation as simple as possible.


Let the trapezoid be ABCD, with the bases a = AB and b = CD.
Let O be the intersection point of diagonals.

Then the triangles AOB and DOC are similar. It is an elementary statement, so let take it with no proof.

The bases of these triangles, AB and DC, are in proportion 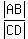 abs%28AB%29%2Fabs%28CD%29 = a%2Fb.


Next, since a trapezoid is not a parallelogram, a =/= b; therefore a%2Fb is not equal to 1.

It means that in triangles AOB and DOC the altitudes OE and OF, drawn from the point O to their bases AB and CD, 
are of different lengths.


From the other side, the midline of the trapezoid ABSD, cuts the altitude EF of the trapezoid in two congruent pieces.

    ( It is true for any trapezoid (!) )


This contradiction explains, why the bases of a trapezoid and its midline are not concurrent.

Solved.