Question 1147573: A playground has an area of 456 meters and a perimeter of 100 meters. How long and wide is it?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
A playground has an area of 456  meters and a perimeter of 100 meters. How long and wide is it?
~~~~~~~~~~~~~~~~~~~
Traditional way to solve it is THIS :
Let W be the width.
Then the length is 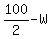 = 50-W.
The area is
W*(50-W) = 456.
and you need to solve this quadratic equation, which I leave to you.
This way is traditional and boring.
I will show you now another way, unexpected, fresh and elegant.
The sum of the width and the length is 50.
Consider the value of  = 25, which is the average of the length and the width.
It is equally remoted from the length and the width :
25 = W + x = L - x (1)
where "x" is some value, unknown to you now.
From (1), W = 25-x, L = 25+x and the area = L*W = (25+x)*(25-x) =  -  ,
so you have this equation
625 - x^2 = 456.
Then x^2 = 625 - 456 = 169, so x =  = 13.
ANSWER. The length of the rectangle is 25+13 = 38 meters. The width of the rectangle is 25-13 = 12 meters.
CHECK. 38*12 = 456 square meters. ! Correct !
It is the way to solve such problems mentally, without using equations.
Solved.
------------------
To see many other similar solved problems, look into the lessons
- Problems on the area and the dimensions of a rectangle
- Three methods to find the dimensions of a rectangle when its perimeter and the area are given
- Three methods to find the dimensions of a rectangle when its area and the difference of two dimensions are given
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic
"Dimensions and the area of rectangles and circles and their elements".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn shows a clever way of solving a problem like this. Two numbers add to 50 and have a product of 456; so call the two numbers 25+x and 25-x and solve the equation
That is a nice shortcut, because the product on the left is 625-x^2, making it relatively easy to solve the problem.
For many students, it will be even faster simply to solve the basic problem by trial and error: find two numbers whose sum is 50 and whose product is 456.
There are many pairs of integers whose sum is 50 and far fewer pairs of integers whose product is 456. So look for a pair of integers with a product of 456 that has a sum of 50.
456*1 obviously not
228*2
152*3
114*4
76*6
57*8
38*12 AHA! That's it!
|
|
|
