Question 1113755: Can a parallelogram always be inscribed in a sircle ? What about square,rhombus, kite and why . I also need reasons.
Found 2 solutions by Edwin McCravy, KMST:
Answer by Edwin McCravy(20059)   (Show Source):
You can put this solution on YOUR website!
For a parallelogram to be inscribable in a circle, its diagonals must
be equal in length and also bisect each other.
This is true of any rectangle:
The two green diagonals are equal in length and bisect each other,
forming 4 radii of a circle.
The diagonals of a parallelogram bisect each other but are not equal unless
the parallelogram happens to be a rectangle.
Therefore a parallelogram cannot be inscribed in a circle unless the
parallelogram happens to be a rectangle.
---------------
Since a square is a rectangle, any square can be inscribed in a circle.
---------------
The diagonals of a rhombus bisect each other but are not equal unless
the rhombus happens to be a square.
Therefore a rhombus cannot be inscribed in a circle unless the
rhombus happens to be a square.
---------------
One case in which a kite can be inscribed in a circle is when the
kite happens to be a square. But that is not the only case:
In order for a kite to be inscribable in a circle, the two congruent
triangles which the long diagonal divides the kite into must be right
triangles. That's because the only triangles inscribable in semicircles
are right triangles.
Therefore a kite cannot be inscribed in a circle unless it contains
two opposite internal right angles.
Edwin
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! You know you can always inscribe a triangle in a circle.
For any triangle,
all perpendicular bisectors of the sides will intersect at the center of its circumcircle.
To find the center of the circumcircle you only need two of those perpendicular bisectors.
A quadrilateral ABCD can be divided into two triangles by diagonal AC.
You can draw the perpendicular bisectors of sides AB and BC.
Where they intersect you find the center, O, of the one and only circumcircle for triangle ABC.
Would point D also be on the circle?
If it is, the perpendicular bisectors of sides AD and DC also have to go through point O.
For a quadrilateral to be inscribed in a circle, the perpendicular bisectors of all four sides have to go through the center of the circle.
The quadrilateral that can be inscribed in a circle is called a cyclical quadrilateral, or an inscribed quadrilateral.
For a rectangle ABCD, the perpendicular bisector of a pair of opposite sides
is the same line connecting the midpoints of those sides. When you do that with both pairs of opposite sides, you just get just two lines that of course have a point in common>
So, a  is a cyclical quadrilateral, and can always be inscribed in a circle.
A  is a special kind of rectangle,so it can always be inscribed in a circle.
A rhombus is a special kind of parallelogram.
A rhombus is also a special kind of kite, but a kite can only be a parallelogram if it is a rhombus.
Here is a kite that is not a parallelogram:
 > you can see that the short sides are not parallel to the long sides.
A kite and a rhombus have diagonals that are perpendicular to each other, and one of those diagonals is an axis of symmetry.
Some special kites can be inscribed in a circle,
but not all kites can be inscribed in a circle.
Let us figure out what would make them special that way.
If the two diagonals have different lengths, consider the longest one.
It is an axis of symmetry for the kite,
so for that kite to be inscribed in a circle,
that diagonal must be the diameter of the circle.
In that case, each of the two triangles that diagonal divides the quadrilateral into
is inscribed in the circle and has the circle diameter for its longest side. The inscribed angle opposite that side intercepts half a circle,
so it is a right angle.
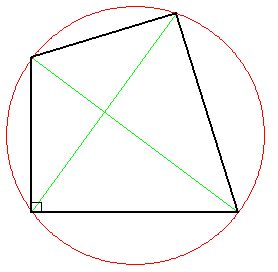
For a kite to be a cyclical quadrilateral, it must have two right angles,
which will be at the ends of a diameter that is not the longest diameter.
Here is a kite that can be inscribed in a circle:
|
|
|
