Question 1099767: a) A rectangular pen is build with one side against a barn. If 2100 m of fencing are used for the other three sides of the pen, what dimensions maximize the area of the pen?
b) A rancher plans to make four identical and adjacent rectangular pens against a barn, each with an area of 400m^2. What are the dimensions of each pen that minimize the amount of fence that must be used?
Found 3 solutions by josmiceli, KMST, ikleyn:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I see the first question as a quadratic function question,
although you need to know enough geometry to understand what a rectangle is.
The second question, looks more like a calculus question
a)  The area The area  of that pen (in square meters) is of that pen (in square meters) is  . .
You should recognize that as a quadratic function,
which graphs as a parabola, looking like this:
 , with two zeros and a maximum exactly midway between them. , with two zeros and a maximum exactly midway between them.
Re-writing it as  shows you clearly that shows you clearly that
 for for  and and  , ,
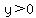 in between, for in between, for 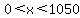 , ,
and the maximum is at 
The dimensions that maximize the area are
 for the length of each of the two fencing sides attached to the barn wall, and for the length of each of the two fencing sides attached to the barn wall, and
 for the length of of the fencing side parallel to the barn wall. for the length of of the fencing side parallel to the barn wall.
b) If we design something with four identical pens, like this:
 , where , where  and and  are lengths in m, are lengths in m,
we know that  <---> <--->  , ,
and that makes the total length of fence needed,  , in m , in m
 . .
Maybe you are supposed to use a graphing calculator to find that the minimum for  happens at approximately happens at approximately  , ,
and you could tell the farmer to use 5 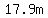 length of fencing perpendicular to the barn wall, length of fencing perpendicular to the barn wall,
attached to a  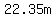 length parallel to the wall. length parallel to the wall.
Using calculus, you would find that the derivative is
 . .
As 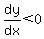 for for 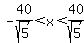 , ,
 for for  , and , and 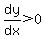 for for 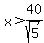 , ,
the function decreases for  to a minimum at to a minimum at  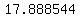 , and increases for , and increases for 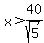 . .
If there is another alternative approach, let me know.
Answer by ikleyn(52798)   (Show Source): (Show Source):
|
|
|