Question 1004217: A 120º arc of a circle has end points (√6,0) and (0, -√6). How long is radius of this circle (in simplest form).
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Points 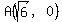 and and 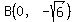 both are at distance both are at distance  from from  , the origin. , the origin.
So, triangle 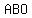 is a right isosceles triangle, with is a right isosceles triangle, with 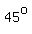 angles at angles at  and and  . .
Points  and and  are on the same arc of a circle of radius are on the same arc of a circle of radius  , ,
so both are at distance  from the center of the circle, from the center of the circle,  . .
Since the center is at the same distance from  and and  , ,
the center is on the perpendicular bisector of  , ,
which contains  , the midpoint of , the midpoint of  . .
The perpendicular bisector of the base of an isosceles triangle passes through the vertex,
so the perpendicular bisector of AB is  . .
The distance from  to to  is is
 , ,
so  . .
Adding point  to the sketch and drawing isosceles triangle to the sketch and drawing isosceles triangle  we get we get

  , and as , and as  is an isosceles triangle, is an isosceles triangle,
altitude  splits it into two congruent splits it into two congruent 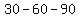 triangles: triangles:  and and  . .
  , and , and  . .
Substituting the measures we know
 , and since , and since  , ,
 --> --> . .
|
|
|