Tutors Answer Your Questions about Geometry Word Problems (FREE)
Question 574963: a pie-shaped (triangular) lake-front lot has a perimeter of 1200 ft. One side is 200 ft longer than the shortest side, while the third side is 400 feet longer than the shortest side. What are the lengths of all three sides?
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In his post, tutor @Theo obtained the solution for the side lengths of the "triangle":
200 ft, 400 ft and 600 ft.
His solution is correct, but he didn't noticed that this triangle is degenerated and, actually,
is not a triangle, since the triangle inequalities are not held.
So, I am warning a reader, that this problem is defective, since it produces
a degenerated triangle, which is not a triangle, at all.
Question 477556: A square has an area of x^2 + 6x + 9 find the length of a side. Make a sketch of the square Please help
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A square has an area of x^2 + 6x + 9. Find the length of a side. Make a sketch of the square Please help
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Tutor @Theo' solution is many words.
I don't like toooo wordy solutions: I think that too wordy explanations are bad style to teach Math.
So, I will write another solution, much shorter and, I believe, more educative.
The expression x^2 + 6x + 9 represents an algebraic perfect square 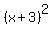 .
So, the area of the square is .
So, the area of the square is 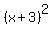 square units.
Hence, the side length of this square is square root of this perfect square square units.
Hence, the side length of this square is square root of this perfect square 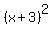 .
So, our first desire is to declare that the side length is (x+3) units.
But it would be too hastily and not always correct.
The reason is that this expression (x+3) can be negative, since we don't know what 'x' is.
Meanwhile, the length of the square must be positive due to the meaning of this notion/conception.
Therefore, more accurate is to write .
So, our first desire is to declare that the side length is (x+3) units.
But it would be too hastily and not always correct.
The reason is that this expression (x+3) can be negative, since we don't know what 'x' is.
Meanwhile, the length of the square must be positive due to the meaning of this notion/conception.
Therefore, more accurate is to write 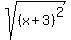 = |x+3| , using the absolute value.
This form is universally correct for all possible values of 'x'.
ANSWER. If the area of a square is x^2 + 6x + 9 square units, then the side of the square is |x+3| units. = |x+3| , using the absolute value.
This form is universally correct for all possible values of 'x'.
ANSWER. If the area of a square is x^2 + 6x + 9 square units, then the side of the square is |x+3| units.
Solved, with complete explanations in compact form.
Question 488212: The perimeter of this block of land is 72 m. Find:
a the length of the block
b the area of the block.
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The perimeter of this block of land is 72 m. Find:
(a) the length of the block
(b) the area of the block.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is incomplete and can not be solved/answered.
Before submitting to this forum, read your posts attentively
and prepare them as accurately as it should be done.
Question 495218: Please help me solve the word problem using
The Rational Zero Theorem
An open metal tank is to be made from a rectangular piece of stainless steel that measures 12 by 6 feet, by cutting out squares of the same size from each corner and bending up the sides. If the volume of the tank is to be 50 ft^3 , how large the square should be cut from each corner?
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Please help me solve the word problem using
The Rational Zero Theorem
An open metal tank is to be made from a rectangular piece of stainless steel that measures 12 by 6 feet,
by cutting out squares of the same size from each corner and bending up the sides.
If the volume of the tank is to be 50 ft^3 , how large the square should be cut from each corner?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I plotted the graph V(x) = (12-2x)*(6-2x)*x for the volume as a function of the size x
of the cut squares at the corners.
I used free of charge online plotting tool www.desmos.com/calculator
You can see the plot under this link
https://www.desmos.com/calculator/9ie79ro4n0
https://www.desmos.com/calculator/9ie79ro4n0
The plot shows that the maximum possible volume is about 41.57 cubic feet
and can not be more than that.
So, your problem is posed INCORRECTLY: the volume of 50 ft^3 CAN NOT be reached.
As presented in the post, this problem is TOTALLY FALSE and FATALLY DEFECTIVE.
A reprimand to the creator of this task.
Question 556812: ANGLE ABE AND ANGLE CBD ARE VERTICAL ANGLES AND BOTH ARE COMPLEMENTARY WITH ANGLE FGH, IF m ANGLE ABE = (3x-1) AND m ANGLE FGH = (4x), what is m ANGLE CBD?
THIS IS THE CORRECT QUESTION..MESSED UP THE ONE BEFORE THIS
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
ANGLE ABE AND ANGLE CBD ARE VERTICAL ANGLES AND BOTH ARE COMPLEMENTARY WITH ANGLE FGH,
IF m ANGLE ABE = (3x-1) AND m ANGLE FGH = (4x), what is m ANGLE CBD?
~~~~~~~~~~~~~~~~~~~~~~~~
Calculations in the post by tutor @Theo are incorrect.
I came to bring a correct solution.
if angle ABE and CBD are vertical angles, then their measure are equal.
if angle ABE is equal to (3x-1) and angle FGH = (4x), then angle CBD must also be equal to (3x-1).
to find the value of x, we use the equation of angle ABE + angle FGH = 90 degrees because they are complementary.
since ABE = 3x-1 and FGH = 4x, this means that:
3x-1 + 4x = 90 degrees
combine like terms to get:
7x-1 = 90
add 1 to both sides of the equation to get:
7x = 91
divide both sides of the equation by 7 to get:
x = 91/7 = 13.
angle FGH is equal to 4x which makes it equal to 4*13 = 52 degrees.
angle ABE is equal to 3x-1 which makes it equal to 3*13-1 = 38 degrees.
add them together to get 90 degrees
the numbers check out.
angle ABE is equal to 38 degrees
angle CBD is equal to angle ABE and so is equal to the same.
ANSWER. Angle CBD is 38 degrees..
--------------------------
Solved correctly.
Question 1165224: Miles takes a 350-mile round-trip flight to visit his parents. To qualify for Gold status at Awesome Airlines, one must fly at least 4200 and less than 15400 miles each year. How many times would Miles need to visit his parents each year to attain Gold status? Express your answer in interval notation.
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1168317: The length of the base of the triangular sheet of canvass above the door of the tent is 3 ft. more than its height (altitude). The area is 5 ft2. Find the height and the length of the base of the triangle.
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The length of the base of the triangular sheet of canvass above the door of the tent is 3 ft. more
than its height (altitude). The area is 5 ft2. Find the height and the length of the base of the triangle.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, you may forget about the tent, about the canvass and about the door,
since they are not relevant to the problem.
What is relevant, is the shape of the figure, which is a triangle.
Let x be the altitude of the triangle (in feet);
then the base of this triangle is (x+3) feet.
Write the area equation for the triangle
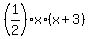 = 5 square feet,
or
x*(x+3) = 5*2 = 10 square feet.
From this equation, you can guess the solution mentally: it is x = 2 feet.
ANSWER. The altitude of the triangle is 2 ft; the base of the triangle is 5 ft. = 5 square feet,
or
x*(x+3) = 5*2 = 10 square feet.
From this equation, you can guess the solution mentally: it is x = 2 feet.
ANSWER. The altitude of the triangle is 2 ft; the base of the triangle is 5 ft.
Solved.
Question 1170888: The triangles ABC and XYZ are similar. The side AB is 5 cm long. The sides BC and
YZ are 7 cm and 3 cm longer than the side XY, respectively. Find the length of XY.
Found 2 solutions by MathTherapy, ikleyn:
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The triangles ABC and XYZ are similar. The side AB is 5 cm long. The sides BC and
YZ are 7 cm and 3 cm longer than the side XY, respectively. Find the length of XY.
 .
Let XY = z
With the 2 Δs being SIMILAR, AB and BC correspond to XY and YZ, respectively
Since BC is 7 cm longer than XY, then BC = XY + 7, or z + 7
Also, since YZ is 3 cm longer than XY, then YZ = XY + 3, or z + 3
With BC being LONGER (XY + 7, or z + 7) than YZ (XY + 3, or z + 3), obviously ΔABC is the LARGER of the 2 .
Let XY = z
With the 2 Δs being SIMILAR, AB and BC correspond to XY and YZ, respectively
Since BC is 7 cm longer than XY, then BC = XY + 7, or z + 7
Also, since YZ is 3 cm longer than XY, then YZ = XY + 3, or z + 3
With BC being LONGER (XY + 7, or z + 7) than YZ (XY + 3, or z + 3), obviously ΔABC is the LARGER of the 2

 <==== Using the former SIMILARITY-PROPORTION <==== Using the former SIMILARITY-PROPORTION

 ---- Cross-multiplying ---- Cross-multiplying

 (z - 3)(z + 5) = 0
z(XY) = 3 cm OR z = - 5 (ignore)
(z - 3)(z + 5) = 0
z(XY) = 3 cm OR z = - 5 (ignore)
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1209920: It has been done before on this website but the question was wrong:
Two identical squares with side of (1+sqrt(2))m overlap to form a regular octagon. What is the area of the octagon?
Answer by greenestamps(13216)   (Show Source): (Show Source):
Question 1173661: Triangle A, B and C are three points on a horizontal field. A is due west of B, the bearing of B from C is 125 degrees, AB = 430m and BC = 460m.
At a certain instant, a hot air balloon is at a point which is directly above C.Given that the angle of elevation of the hot air balloon from B is 5.2 degrees, find the angle of elevation of the hot air balloon from A.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break this problem down step-by-step.
**1. Draw a Diagram**
* Draw a horizontal line segment AB, with A to the left of B.
* Draw a line segment BC, where the bearing of B from C is 125 degrees. This means the angle between the north line from C and the line CB is 125 degrees. Since A is west of B, the angle ACB is 180 - 125 - 90 = 35 degrees.
* Draw a vertical line segment from C upwards to represent the hot air balloon's position. Let's call this point D.
* Connect BD and AD.
**2. Use the Law of Cosines to Find AC**
* We know AB = 430m, BC = 460m, and angle ACB = 35 degrees.
* Use the law of cosines: AC² = AB² + BC² - 2(AB)(BC)cos(ACB)
* AC² = 430² + 460² - 2(430)(460)cos(35°)
* AC² = 184900 + 211600 - 395600cos(35°)
* AC² = 396500 - 324484.7
* AC² = 72015.3
* AC = √72015.3 ≈ 268.36 m
**3. Find the Height of the Hot Air Balloon (CD)**
* The angle of elevation of the hot air balloon from B is 5.2 degrees.
* We have a right triangle BCD.
* tan(5.2°) = CD / BC
* CD = BC * tan(5.2°)
* CD = 460 * tan(5.2°)
* CD ≈ 460 * 0.0909
* CD ≈ 41.81 m
**4. Find the Angle of Elevation from A**
* We have a right triangle ACD.
* We know AC ≈ 268.36 m and CD ≈ 41.81 m.
* tan(angle CAD) = CD / AC
* tan(angle CAD) = 41.81 / 268.36
* tan(angle CAD) ≈ 0.1558
* angle CAD = arctan(0.1558) ≈ 8.85 degrees
**Therefore, the angle of elevation of the hot air balloon from A is approximately 8.85 degrees.**
Question 1173737: Airport B is 320 miles from airport A on a bearing of S40°E. A pilot wishes to fly from A to B, but to avoid a storm must first fly due East at a speed of 210 mph for an hour, and then from this point (call it C) turns to fly to B. Find the distance, to the nearest mile, and the bearing, to the nearest degree, that the pilot must fly to airport B?
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step.
**1. Visualize the Problem**
* **A to B:** 320 miles, bearing S40°E
* **A to C:** Due East, 210 mph for 1 hour
* **C to B:** We need to find the distance and bearing.
**2. Calculate the Distance from A to C**
* Distance = Speed * Time
* Distance AC = 210 mph * 1 hour = 210 miles
**3. Set Up a Coordinate System**
* Let A be the origin (0, 0).
* Since AC is due East, point C is (210, 0).
* To find the coordinates of B, we need to use the distance and bearing from A to B.
**4. Find the Coordinates of B**
* Bearing S40°E means 40 degrees east of south.
* We can use trigonometry to find the coordinates:
* x-coordinate (Eastward): 320 * sin(40°)
* y-coordinate (Southward): 320 * cos(40°)
* Calculate:
* x = 320 * sin(40°) ≈ 205.67 miles
* y = 320 * cos(40°) ≈ 245.13 miles
* Since it's S40°E, the coordinates of B are (205.67, -245.13).
**5. Find the Distance from C to B**
* Use the distance formula:
* CB = √[(x2 - x1)² + (y2 - y1)²]
* CB = √[(205.67 - 210)² + (-245.13 - 0)²]
* CB = √[(-4.33)² + (-245.13)²]
* CB = √[18.75 + 60088.66]
* CB = √60107.41
* CB ≈ 245.17 miles
* Rounded to the nearest mile, CB ≈ 245 miles.
**6. Find the Bearing from C to B**
* We need to find the angle between the East direction from C and the line CB.
* Use the tangent function:
* tan(θ) = |y-coordinate| / |x-coordinate|
* tan(θ) = 245.13 / 4.33
* tan(θ) ≈ 56.61
* θ = arctan(56.61) ≈ 88.99 degrees
* Since B is south and slightly west of C, the bearing is approximately S89°W.
**Final Answers**
* **Distance (CB):** Approximately 245 miles
* **Bearing (C to B):** Approximately S89°W
Question 1180959: In a circle with diameter of 12 inches, a regular five-pointed star is inscribed. What is the area of thet part not covered by the star
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to approach this problem, although finding the exact area of the star and the uncovered portion is complex and usually requires numerical methods or a good approximation:
1. **Area of the Circle:** The diameter is 12 inches, so the radius is 6 inches. The area of the circle is πr² = π(6²) = 36π square inches.
2. **Area of the Star:** Calculating the exact area of a regular pentagram (five-pointed star) inscribed in a circle is tricky. It involves trigonometry and can be quite involved. There's no simple formula. The area depends on the radius of the circle.
3. **Area of the Uncovered Portion:** Once you have the area of the star, you subtract it from the area of the circle to find the area of the part not covered by the star.
**Why it's complex:** The points of the star divide the circumference of the circle in a specific ratio, and the sides of the star form chords within the circle. Calculating the lengths of these chords and the areas of the triangles that make up the star requires a good understanding of trigonometry (sine, cosine, and potentially the Law of Cosines).
**Approximation/Numerical Methods:** The most practical way to get a numerical answer is to use a calculator or software that can handle trigonometric functions and potentially break the star into simpler shapes (triangles) to calculate the area.
**General Idea (Without Exact Calculation):**
* The area of the star will be *less* than the area of the circle.
* The uncovered area will be the difference between the circle's area and the star's area.
**If you had the area of the star (let's call it 'S'), the uncovered area would be 36π - S.**
**In summary:** While the concept is straightforward, the actual calculation of the star's area requires more advanced math than is typically encountered in basic geometry. You'd likely need a calculator or a resource with the specific formula for a pentagram's area.
Question 1186123: The angular elevation of a tower CD at a place A due south of it is 60°; and at a place B due west of A, the elevation is 30°. If AB = 3 km, what is the height of the tower?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Let points A,B,C be placed on the ground.
A and B are the observation points.
C is the base of the tower.
D is the top of the tower.

x = distance from A to C
y = distance from B to C
h = height of the tower = distance from C to D
Each distance is in kilometers and each is positive.
Focus on right triangle CAD.
tan(angle) = opposite/adjacent
tan(angle CAD) = CD/CA
tan(60) = h/x
h = x*tan(60)
h = x*sqrt(3)
Now focus on right triangle CBD.
tan(angle) = opposite/adjacent
tan(angle CBD) = CD/CB
tan(30) = h/y
h = y*tan(30)
x*sqrt(3) = y*tan(30) ........... plugged in h = x*sqrt(3)
x*sqrt(3) = y*(1/sqrt(3))
y = x*sqrt(3)*sqrt(3)
y = 3x
Focus on right triangle ABC that is entirely on the ground.
The horizontal leg (that runs east/west) is AB = 3 km.
The leg running north/south is AC = x and the hypotenuse is BC = y = 3x
Use the Pythagorean Theorem for right triangle ABC.
(AB)^2 + (AC)^2 = (BC)^2
(3)^2 + (x)^2 = (3x)^2
9 + x^2 = 9x^2
9x^2-x^2 = 9
8x^2 = 9
x^2 = 9/8
x = sqrt(9/8)
Since x > 0 we ignore the minus of the plus/minus.
Then,
h = x*sqrt(3)
h = sqrt(9/8)*sqrt(3)
h = sqrt((9/8)*3)
h = sqrt(27/8)
h = sqrt(27)/sqrt(8)
h = (3*sqrt(3))/(2*sqrt(2))
h = (3*sqrt(3)*sqrt(2))/(2*sqrt(2)*sqrt(2)) .... rationalizing denominator
h = (3*sqrt(3*2))/(2*2)
h = (3/4)*sqrt(6) km is the exact answer
h = 1.837117 km approximately
The approximate answer varies depending how you round.
------------------------------------------------------------------------------
Another way to solve:
Focus on triangle CAD
tan(60) = h/x
x = h/tan(60)
x = h/sqrt(3)
Focus on triangle CBD
tan(30) = h/y
y = h/tan(30)
y = h*sqrt(3)
The last triangle to focus on is ABC.
It has legs AB = 3 and AC = x. The hypotenuse is BC = y.
Use the Pythagorean Theorem
(AB)^2 + (AC)^2 = (BC)^2
3^2 + x^2 = y^2
3^2 + (h/sqrt(3))^2 = (h*sqrt(3))^2
9 + (h^2)/3 = h^2*3
27 + h^2 = 9h^2
9h^2-h^2 = 27
8h^2 = 27
h^2 = 27/8
h = sqrt(27/8)
The steps from here are the same as the previous section.
You should arrive at
h = (3/4)*sqrt(6) km = 1.837117 km approximately
As of 2025, the world's tallest building is the Burj Khalifa at around 828 meters tall.
The answer we got is over 1000 meters taller, so tower CD is definitely breaking records.
I don't know how realistic it is for a tower to be this tall.
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1188293: The direction of a railroad cut is perpendicular to the horizontal ridge AB. Assuming the sides of the ridge to be plane surfaces making equal angles with the horizontal, find the amount of earth removed if the base is a rectangle, 30 ft. wide by 400 ft. long, in a plane 60 ft. below the line AB; and the sides of the cut are inclined 45 degrees to the horizontal.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to calculate the volume of earth removed:
**1. Visualize the Problem:**
Imagine a horizontal ridge AB. The railroad cut goes straight down, perpendicular to AB. The sides of the cut slope inwards at a 45-degree angle. The base of the cut is a rectangle.
**2. Cross-Sectional Area:**
The key is to find the cross-sectional area of the cut. Because the sides are inclined at 45 degrees, and the cut is perpendicular to the ridge, the cross-section will be a trapezoid.
* **Base of trapezoid:** This is the width of the rectangular base of the cut, which is 30 ft.
* **Height of trapezoid:** This is the vertical depth of the cut, which is 60 ft.
* **Top of trapezoid:** Because the sides are at 45 degrees, the top of the trapezoid is wider than the base. For each side, the additional width is equal to the vertical depth (60 ft). Since there are two sides, the top of the trapezoid is 30 ft + 2 * 60 ft = 150 ft.
**3. Calculate the Area of the Trapezoid:**
Area = (1/2) * (base1 + base2) * height
Area = (1/2) * (30 ft + 150 ft) * 60 ft
Area = (1/2) * 180 ft * 60 ft
Area = 5400 sq ft
**4. Calculate the Volume:**
Volume = Area of cross-section * length
Volume = 5400 sq ft * 400 ft
Volume = 2,160,000 cu ft
**Answer:**
The amount of earth removed is 2,160,000 cubic feet.
Question 1209516: my friend drives north for 4 miles and my other friend drives west for 5 miles, what is the distance between my friends.
Found 2 solutions by math_tutor2020, josgarithmetic:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by josgarithmetic(39630)  (Show Source): (Show Source):
Question 1209061: Verify that the points (0,0), (a,0) and (c,d) are the vertices of an equilateral triangle.
Note: c = (a/2) and d = (a•sqrt{3})/2
Then show that the midpoints of the 3 sides are the vertices of a second equilateral triangle.
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Verify Equilateral Triangle**
* **Points:**
* A: (0, 0)
* B: (a, 0)
* C: (c, d) = (a/2, (a√3)/2)
* **Distances:**
* AB = √[(a - 0)² + (0 - 0)²] = √a² = a
* BC = √[(a/2 - a)² + ((a√3)/2 - 0)²] = √[(-a/2)² + (a√3/2)²] = √(a²/4 + 3a²/4) = √(4a²/4) = a
* AC = √[(a/2 - 0)² + ((a√3)/2 - 0)²] = √[(a/2)² + (a√3/2)²] = √(a²/4 + 3a²/4) = √(4a²/4) = a
Since AB = BC = AC = a, the points A, B, and C form an equilateral triangle.
**2. Find Midpoints**
* **Midpoint of AB (M1):**
* [(0 + a)/2, (0 + 0)/2] = (a/2, 0)
* **Midpoint of BC (M2):**
* [(a + a/2)/2, (0 + (a√3)/2)/2] = (3a/4, (a√3)/4)
* **Midpoint of AC (M3):**
* [(0 + a/2)/2, (0 + (a√3)/2)/2] = (a/4, (a√3)/4)
**3. Verify Equilateral Triangle for Midpoints**
* **M1M2:**
* √[((3a/4) - (a/2))² + ((a√3)/4 - 0)²] = √[(a/4)² + (a√3/4)²] = √(a²/16 + 3a²/16) = √(4a²/16) = a/2
* **M2M3:**
* √[((a/4) - (3a/4))² + ((a√3)/4 - (a√3)/4)²] = √[(-a/2)² + 0²] = a/2
* **M3M1:**
* √[((a/2) - (a/4))² + (0 - (a√3)/4)²] = √[(a/4)² + (a√3/4)²] = √(a²/16 + 3a²/16) = a/2
Since M1M2 = M2M3 = M3M1 = a/2, the midpoints M1, M2, and M3 also form an equilateral triangle.
**Therefore, it is proven that if the points (0, 0), (a, 0), and (c, d) (where c = a/2 and d = (a√3)/2) are the vertices of an equilateral triangle, then the midpoints of the sides of this triangle also form an equilateral triangle.**
Question 1209079: Overlay a rectangular coordinate system on a Little League baseball diamond so that the origin is at home plate, the positive x-axis lies in the direction from home plate to first base, and the positive y-axis lies in the direction from home plate to third base.
(a) What are the coordinates of first base, second base, and third base? Use feet as the unit of measurement.
(b) If the right fielder is located at (180,20), how far is it from the right fielder to second base?
(c) If the center fielder is located at (220,220), how far is it from the center fielder to third base?
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a) Coordinates of Bases**
* **First Base:** (90 feet, 0 feet)
* **Second Base:** (90 feet, 90 feet)
* **Third Base:** (0 feet, 90 feet)
**b) Distance from Right Fielder to Second Base**
* Right Fielder: (180, 20)
* Second Base: (90, 90)
* **Distance Formula:**
* Distance = √[(x2 - x1)² + (y2 - y1)²]
* **Calculate Distance:**
* Distance = √[(90 - 180)² + (90 - 20)²]
* Distance = √[(-90)² + (70)²]
* Distance = √(8100 + 4900)
* Distance = √13000
* Distance ≈ 114 feet
**c) Distance from Center Fielder to Third Base**
* Center Fielder: (220, 220)
* Third Base: (0, 90)
* **Calculate Distance:**
* Distance = √[(0 - 220)² + (90 - 220)²]
* Distance = √[(-220)² + (-130)²]
* Distance = √(48400 + 16900)
* Distance = √65300
* Distance ≈ 255.54 feet
**In summary:**
* **First Base:** (90, 0)
* **Second Base:** (90, 90)
* **Third Base:** (0, 90)
* **Distance from Right Fielder to Second Base:** ≈ 114 feet
* **Distance from Center Fielder to Third Base:** ≈ 255.54 feet
Question 1199923: Find the maximum number of non-overlapping regions into which 10 additional straight lines can subdivide this figure.
https://ibb.co/gPRWCRR
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Initial Regions:**
* The rectangle is already divided into 4 smaller rectangles.
**2. Effect of Each Line:**
* **First Line:** At most, it can intersect existing lines twice, creating 2 new regions.
* **Second Line:** At most, it can intersect the first line and existing lines twice, creating 3 new regions.
* **Third Line:** At most, it can intersect the first two lines and existing lines twice, creating 4 new regions.
* **And so on...**
**3. General Pattern:**
* Each subsequent line can potentially intersect all the previous lines at most once, creating one additional region for each intersection.
**4. Maximum Regions:**
* **Initial Regions:** 4
* **First Line:** 4 + 2 = 6 regions
* **Second Line:** 6 + 3 = 9 regions
* **Third Line:** 9 + 4 = 13 regions
* **Fourth Line:** 13 + 5 = 18 regions
* **Fifth Line:** 18 + 6 = 24 regions
* **Sixth Line:** 24 + 7 = 31 regions
* **Seventh Line:** 31 + 8 = 39 regions
* **Eighth Line:** 39 + 9 = 48 regions
* **Ninth Line:** 48 + 10 = 58 regions
* **Tenth Line:** 58 + 11 = 69 regions
**Therefore, the maximum number of non-overlapping regions into which 10 additional straight lines can subdivide the figure is 69.**
**Note:** This assumes that the lines are strategically placed to maximize the number of intersections and, consequently, the number of regions.
Question 1199950: Find the maximum number of non-overlapping regions into which 10 additional straight lines can subdivide this figure.
Figure: https://ibb.co/99bk08m
Thanks so much!
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Initial Regions:**
* The rectangle is already divided into 4 smaller rectangles.
**2. Effect of Each Line:**
* **First Line:** At most, it can intersect existing lines twice, creating 2 new regions.
* **Second Line:** At most, it can intersect the first line and existing lines twice, creating 3 new regions.
* **Third Line:** At most, it can intersect the first two lines and existing lines twice, creating 4 new regions.
* **And so on...**
**3. General Pattern:**
* Each subsequent line can potentially intersect all the previous lines at most once, creating one additional region for each intersection.
**4. Maximum Regions:**
* **Initial Regions:** 4
* **First Line:** 4 + 2 = 6 regions
* **Second Line:** 6 + 3 = 9 regions
* **Third Line:** 9 + 4 = 13 regions
* **Fourth Line:** 13 + 5 = 18 regions
* **Fifth Line:** 18 + 6 = 24 regions
* **Sixth Line:** 24 + 7 = 31 regions
* **Seventh Line:** 31 + 8 = 39 regions
* **Eighth Line:** 39 + 9 = 48 regions
* **Ninth Line:** 48 + 10 = 58 regions
* **Tenth Line:** 58 + 11 = 69 regions
**Therefore, the maximum number of non-overlapping regions into which 10 additional straight lines can subdivide the figure is 69.**
**Note:** This assumes that the lines are strategically placed to maximize the number of intersections and, consequently, the number of regions.
Question 1200029: Find the maximum number of non-overlapping regions into which 10 additional straight lines can subdivide this figure.
Figure: https://ibb.co/99bk08m
Thanks so much!
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Initial Regions:**
* The rectangle is already divided into 4 smaller rectangles.
**2. Effect of Each Line:**
* **First Line:** At most, it can intersect existing lines twice, creating 2 new regions.
* **Second Line:** At most, it can intersect the first line and existing lines twice, creating 3 new regions.
* **Third Line:** At most, it can intersect the first two lines and existing lines twice, creating 4 new regions.
* **And so on...**
**3. General Pattern:**
* Each subsequent line can potentially intersect all the previous lines at most once, creating one additional region for each intersection.
**4. Maximum Regions:**
* **Initial Regions:** 4
* **First Line:** 4 + 2 = 6 regions
* **Second Line:** 6 + 3 = 9 regions
* **Third Line:** 9 + 4 = 13 regions
* **Fourth Line:** 13 + 5 = 18 regions
* **Fifth Line:** 18 + 6 = 24 regions
* **Sixth Line:** 24 + 7 = 31 regions
* **Seventh Line:** 31 + 8 = 39 regions
* **Eighth Line:** 39 + 9 = 48 regions
* **Ninth Line:** 48 + 10 = 58 regions
* **Tenth Line:** 58 + 11 = 69 regions
**Therefore, the maximum number of non-overlapping regions into which 10 additional straight lines can subdivide the figure is 69.**
**Note:** This assumes that the lines are strategically placed to maximize the number of intersections and, consequently, the number of regions.
Question 1209064: Find all points on the x-axis and y-axis that are 6 units from the point (4,-3).
Answer by timofer(107)  (Show Source): (Show Source):
You can put this solution on YOUR website! An unknown point on x axis, (x,0)
6 units from (4,-3)

An unknown point on y axis, (0,y)
6 units from (4,-3)

Those are based on Distance Formula.
Solve those.
Question 1209076: A hot-air balloon, headed due east at an average speed of 25 miles per hour and at a constant altitude of 125 feet, passes over an intersection. Find the expression for the distance d (measured in feet) from the balloon to the intersection t seconds later.
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1209077: When a draftsman draws three lines that are to intersect at one point, the lines may not intersect as intended and subsequently will form an error triangle. If this error triangle is long and thin, one estimate for the location of the desired point is the midpoint of the shortest side.
A. Find an estimate for the desired intersection point.
B. Find the length of the median for the midpoint found in part A.
C. Show this error triangle on the xy-plane.
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I see many words in this post, written in good English on behalf of the draftsman,
but I do not see a mathematical problem in it.
May be, I should read it using microscope or telescope ?
Or Artificial Intelligence ?
Or all three devices at a time ?
Question 1209078: A Dodge Neon and a Mack truck leave an intersection at the same time.The Neon heads east at an average speed of 40 miles per hour, while the truck heads south at an average speed of 50 miles per hour. Find an expression for their distance apart d (in miles) at the end of t hours.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Hint:

distance = rate*time
The Neon travels a distance 40t due to the equation above.
Meanwhile the Mack truck travels a distance of 50t.
The goal is to find the length of the hypotenuse.
The answer is some expression in terms of t.
Another hint is the Pythagorean Theorem 
Question 1209060: Find the midpoint of each diagonal of a square whose side length is x. Is it true that the diagonals of a square intersect at their midpoint?
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(a) Find the midpoint of each diagonal of a square whose side length is x.
(b) Is it true that the diagonals of a square intersect at their midpoint?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
First question (part (a) ) makes no sense.
Regarding the second part (b), the answer with explanations is below.
The diagonals of any parallelogram intersect at their midpoints.
A square is a parallelogram - - - hence, its diagonals intersect at their midpoints.
Question 1209062: The midpoint of the line segment from A to B is (5,-4). If B = (7,-2), what is A?
Found 4 solutions by ikleyn, greenestamps, math_tutor2020, mccravyedwin:
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Point " A " is the mirror reflection of point B in the mirror,
if the mirror is established at the midpoint and directed to point B.
By knowing it, you do the rest mechanically.
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
From the midpoint (5,-4) to B(7,-2) is 2 units RIGHT from 5 to 7 and 2 units UP from -4 to -2.
To get from the midpoint to A, we need to move the same distances in the opposite directions from the midpoint.
2 units LEFT from 5 is 3; 2 units DOWN from -4 is -6. A is (3,-6).
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
A = (x,y)
B = (7,-2)
M = (5,-4) = midpoint of segment AB.
To find the x coordinate of the midpoint, we add the x coordinates of A and B.
Then divide in half.
(x+7)/2 = 5
I'll let the student solve from here.
Similarly, the y coordinate set up equation would be:
(y-2)/2 = -4
I'll let the student solve from here.
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This is really a look-and-see problem if you have graph paper.
Let's call the midpoint M(5,-4). Notice that M is 2 units left
and 2 units down from B. Since M is the midpoint of AB, you know
that A has to be two units left and 2 units down from M. The
green line MB is half of AB.
 So let's redraw the graph, and you can locate A by observing what point
is 2 units left and 2 units down from M. We'll draw the lower half of AB,
which is AM. So what are the coordinates of A? I don't need to tell you,
right? You can look and see!
So let's redraw the graph, and you can locate A by observing what point
is 2 units left and 2 units down from M. We'll draw the lower half of AB,
which is AM. So what are the coordinates of A? I don't need to tell you,
right? You can look and see!
 Edwin
Edwin
Question 1209063: Find all points having a y-coordinate of -6 whose distance from the point (1,2) is 17.
(a)By using the Pythagorean Theorem.
(b)By using the distance formula.
Found 2 solutions by ikleyn, mccravyedwin:
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find all points having a y-coordinate of -6 whose distance from the point (1,2) is 17.
(a)By using the Pythagorean Theorem.
(b)By using the distance formula.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In the post by Edwin, the solution and the answer are incorrect.
In his solution, Edwin mistakenly used y-coordinate 6 instead of the given -6.
His plot is inadequate, too.
I came to bring a correct solution.
Let's call the given point A = (1,2).
All points having y-coordinate of -6, lie on the horizontal line y = -6.
Vertical distance from the point (1,2) to this line (or simply the distance) is 6+2 = 8 units.
This distance is the length of the perpendicular from this point (1,2) to the line y= -6.
We want to find points C on the line y= -6 such that the distance from A to C is 17 units.
Draw the perpendicular AB from A to line y= -6. The length of this perpendicular is 8 units.
The coordinates of B are (1,-6).
The triangle ABC is a right-angled triangle.
Its diagonal AC has the length of 17 units; its leg AB is of 8 units.
Hence, the leg BC along the line y = -6 is (Pythagoras)
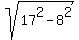 = = 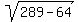 = = 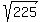 = 15 units.
Thus possible points C are (1+15,-6) = (16,-6) or (1-15,-6) = (-14,-6).
ANSWER. There are two such points C = (16,-6) and C' = (-14,-6). = 15 units.
Thus possible points C are (1+15,-6) = (16,-6) or (1-15,-6) = (-14,-6).
ANSWER. There are two such points C = (16,-6) and C' = (-14,-6).
Solved (correctly).
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The green line is the set of all points having a y-coordinate of 6.
The green circle, with center (1,2) and radius 17, is the set of all points
whose distance from point (1,2) is 17. So the 2 points they have in common
are the only two points having both properties. So the answer will be those
two points.
B is 6 units above the x-axis and A is 2 units above the x-axis, so the
distance AB = 6-2 = 4.
We have AB=4 and AC=17,  .
B is 1 unit farther to the right of the y-axis, so is C, and therefore .
B is 1 unit farther to the right of the y-axis, so is C, and therefore
 That makes C' one unit less to the left of the y-axis, so
That makes C' one unit less to the left of the y-axis, so

 --------------
Distance formula:
Let the point (x,y) [where y=6, which means the point (x,6)] have distance
17 from point (1,2).
Then
--------------
Distance formula:
Let the point (x,y) [where y=6, which means the point (x,6)] have distance
17 from point (1,2).
Then



 Square both sides:
Square both sides:



 Thus the two points are
Thus the two points are
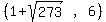 and and 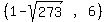 Edwin
Edwin
Question 1209041: Find the midpoint given two points: [(a+b)/2, (c+d)/2] and [(a-b)/2, (c-d)/2].
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
x-coordinate of the midpoint is half of the sum of x-coordinates of the given points
x = 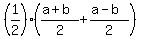 = 0.5a.
y-coordinate of the midpoint is half of the sum of y-coordinates of the given points
x = = 0.5a.
y-coordinate of the midpoint is half of the sum of y-coordinates of the given points
x = 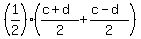 = 0.5c.
Thus the midpoint is (x,y) = (0.5a,0.5c). ANSWER = 0.5c.
Thus the midpoint is (x,y) = (0.5a,0.5c). ANSWER
Solved.
Question 1209044: Find all points having a y-coordinate of -6 whose distance from the point is 17.
(a)By using the Pythagorean Theorem.
(b)By using the distance formula.
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1209027: Find the lengths of the medians of the triangle whose vertices are A = (0.0), B =(6,0), and C = (4,4).
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the lengths of the medians of the triangle whose vertices are A = (0,0), B =(6,0), and C = (4,4).
~~~~~~~~~~~~~~~~~~~~~
The median from A = (0,0) has the opposite end at D = (5,2).
Its length is AD = 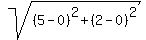 = = 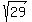 .
The median from B = (6,0) has the opposite end at E = (2,2).
Its length is BE = .
The median from B = (6,0) has the opposite end at E = (2,2).
Its length is BE = 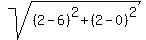 = = 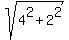 = =  = = 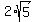 .
The median from C = (4,4) has the opposite end at F = (3,0).
Its length is CF = .
The median from C = (4,4) has the opposite end at F = (3,0).
Its length is CF = 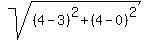 = = 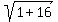 = =  . .
Solved in full.
Question 1209028: If two vertices of an equilateral triangle are (0,0) and (0,4), find the third vertex. How many of these triangles are possible?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The side connecting points A = (0,0) and B = (0,4) is vertical y-axis.
The third vertex C lies on the perpendicular to AB in its midpoint.
The midpoint of AB is the point (0,2).
The perpendicular to AB in its midpoint is horizontal line y= 2.
The altitude of this equilateral triangle has the length  = = 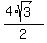 = =  .
This altitude is the distance of the third vertex C from y-axis - hence, it gives x-coordinate of vertex C.
Thus, the point C, which is the third vertex of the triangle, has coordinates (x,y) = (+/- .
This altitude is the distance of the third vertex C from y-axis - hence, it gives x-coordinate of vertex C.
Thus, the point C, which is the third vertex of the triangle, has coordinates (x,y) = (+/- , , ).
So, one version is when triangle ABC lies in the first quadrant. Then its third vertex is (x,y) = ( ).
So, one version is when triangle ABC lies in the first quadrant. Then its third vertex is (x,y) = ( , , ).
Another version is when triangle ABC lies in the second quadrant. Then its third vertex is (x,y) = ( ).
Another version is when triangle ABC lies in the second quadrant. Then its third vertex is (x,y) = (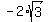 , , ).
So, there are two possible equilateral triangles ABC and two different positions for vertex C. ).
So, there are two possible equilateral triangles ABC and two different positions for vertex C.
Solved.
All you need to know and to use to solve this problem is basic elementary properties of equilateral triangles.
By knowing it and using it, you solve this problem MENTALLY in 10 or 20 seconds.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1209026: Find all points having a y-coordinate of whose distance from the point is 17.
(a)By using the Pythagorean Theorem.
(b)By using the distance formula.
Answer by greenestamps(13216)   (Show Source): (Show Source):
Question 1209013: Find the approximated change in the volume of a
rectangular solid caused by increasing each side by
5%.
15
Answer by timofer(107)  (Show Source): (Show Source):
Question 1209000:
A 39-ounce can of Hills Bros. coffee requires 188.5 square inches of aluminum. If its height is 7 inches, what is its radius?
[Hint: The surface area S of a right cylinder is S = 2pi•r2 + 2pi•rh, where r is the radius, and h is the height.]
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It was solved at this forum many years ago. See the solutions under these links
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.209457.html
https://www.algebra.com/algebra/homework/word/misc/Miscellaneous_Word_Problems.faq.question.146645.html
Question 1208967:
A pond is enclosed by a wooden deck that is 3 feet wide.The fence surrounding the deck is 100 feet long.
(a) If the pond is square, what are its dimensions?
(b) If the pond is rectangular and the length of the pond is to be three times its width, what are its dimensions?
(c) If the pond is circular, what is its diameter?
(d) Which pond has the most area?
Answer by ikleyn(52915)   (Show Source): (Show Source):
Question 1208965: the length of a rectangle is 7 more that 3 times its width. if the perimeter is 38 cm, what is the area, in square centimeters, of the rectangle
Found 2 solutions by mccravyedwin, ikleyn:
Answer by mccravyedwin(409)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If we want to get real picky, in addition to the omission of "centimeter",:
1. The two sentences should begin with capital letters.
2. The word "that" should be "than".
3. The second sentence is a question, and should end with a question mark "?".
Edwin
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Formally, this problem is written incorrectly.
To be correct, the problem must say that this " 7 more " is, actually, " 7 centimeters more ".
Not 7 inches more, not 7 feet more, not 7 yards more, not 7 meters more,
not 7 millimeters more, not 7 kilometers more, and not 7 apples more.
But precisely 7 centimeters more.
In word Math problems, it is  to use numbers without pointing their dimension units. to use numbers without pointing their dimension units.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390, 15391..15435, 15436..15480, 15481..15525, 15526..15570, 15571..15615, 15616..15660, 15661..15705, 15706..15750, 15751..15795, 15796..15840, 15841..15885, 15886..15930, 15931..15975, 15976..16020
|


 .
Let XY = z
With the 2 Δs being SIMILAR, AB and BC correspond to XY and YZ, respectively
Since BC is 7 cm longer than XY, then BC = XY + 7, or z + 7
Also, since YZ is 3 cm longer than XY, then YZ = XY + 3, or z + 3
With BC being LONGER (XY + 7, or z + 7) than YZ (XY + 3, or z + 3), obviously ΔABC is the LARGER of the 2
.
Let XY = z
With the 2 Δs being SIMILAR, AB and BC correspond to XY and YZ, respectively
Since BC is 7 cm longer than XY, then BC = XY + 7, or z + 7
Also, since YZ is 3 cm longer than XY, then YZ = XY + 3, or z + 3
With BC being LONGER (XY + 7, or z + 7) than YZ (XY + 3, or z + 3), obviously ΔABC is the LARGER of the 2



