Question 273725: how could i explain to a teacher how to find the area of a trapazoid?
Found 3 solutions by JBarnum, solver91311, Theo:
Answer by JBarnum(2146)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Probably the same way you would explain it to anyone else. The first thing you would need to do is to determine what the teacher listening to the explanation believes the word "trapezoid" to mean. If s/he is in the UK, s/he might believe the term "trapezoid" refers to a general quadrilateral having no parallel sides. In that case you would politely explain that there is no general method for finding the area of a trapezoid other than dividing the figure into two triangles, attempting to determine the areas of the two triangles, and then summing the two areas. On the other hand, particularly if your audience is from the US, I would say take the average of the measures of the two parallel sides, then multiply that result times the altitude of the trapezoid which is defined as the distance between the two parallel sides.
John

Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! use the formula for a trapezoid.
that formula is:
area = 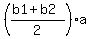
b1 is the top base
b2 is the bottom base
a is the altitude (height) of the trapezoid.
attached reference helps you to see how this works.
http://www.mathopenref.com/trapezoidarea.html
how the formula was derived is a lot more complicated.
if you look at the picture of a trapezoid shown below, you will see that the trapezoid is composed of a rectangle and a triangle on each end.

The trapezoid in the picture is composed of the areas of 1+2+3.
2 is a rectangle.
1 and 3 are triangles.
if you complete a larger rectangle, then you will see that the area of this larger rectangle is composed of the areas of 1+2+3+4+5.
The area of 2 is made by the base b1 * the altitude (a).
The area of 1+2+3+4+5 is made by the base b2 * the altitude (a).
The formula for the area of the trapezoid is a*(b1+b2)/2 which is the same as:
(a*b1)/2 + (a*b2)/2
now a*b1 = the area called 2 which is the area of the smaller rectangle.
now also a*b2 = the area of (1+2+3+4+5) which is the area of the larger rectangle.
based on the previous 2 statements, the area of the trapezoid is equivalent to:
(2/2) + (1+2+3+4+5)/2
this is equivalent to:
the area of (2/2) + the area of (1/2) + (2/2) + (3/2) + (4/2) + (5/2)
now (2/2) + (2/2) = 2 so our formula becomes:
the area of 2 + the areas of (1/2) + (3/2) + (4/2) + (5/2)
we also know that the area of triangle 4 is equivalent to the area of triangle 1.
we also know that the area of triangle 5 is equivalent to the area of triangle 3.
This is because triangle 4 is congruent to triangle 1, and because triangle 5 is congruent to triangle 3. These triangles are congruent by SSS.
what this means is that we can substitute the area of triangle 1 for the area of triangle 4.
what this also means that we can substitute the area of triangle 3 for the area of triangle 5.
our formula of:
area of 2 + areas of (1/2) + (3/2) + (4/2) + (5/2)
can be made into:
area of 2 + areas of (1/2) + (1/2) + (3/2) + (3/2)
this is because 1 and 4 are equivalent, and 3 and 5 are equivalent.
since 1/2 + 1/2 = 1, and since 3/2 + 3/2 = 3, our formula becomes:
2 + 1 + 3.
if we reorder the terms, we get:
1 + 2 + 3 which is the area of our trapezoid.
by looking at each of the piece parts, we have determined that the area of the trapezoid given by the formula:
area = a*(b1+b2)/2
is equivalent to the formula:
area = (a*b1)/2 + (a*b2)/2 which is the area of the smaller rectangle divided by 2 plus the area of the larger rectangle divided by 2.
it's tricky, but it works.
if you can't deal with the complexity of the derivation, then just stick with the formula.
the formula for the area of a trapezoid is equal to (b1+b2)/2 * a.
|
|
|