SOLUTION: the segment joining A(-3, "-2)" and B(-1/2 , 3) is extended to a distance equal to 1/5 of its own length. find the new end point closest to point A

Algebra ->  Formulas -> SOLUTION: the segment joining A(-3, "-2)" and B(-1/2 , 3) is extended to a distance equal to 1/5 of its own length. find the new end point closest to point A      Log On


   

Question 1193681: the segment joining A(-3, "-2)" and B(-1/2 , 3) is extended to a distance equal to 1/5 of its own length. find the new end point closest to point A
Answer by Boreal(15235) About Me  (Show Source):
You can put this solution on YOUR website!
The length of the line is sqrt(difference in x s^2+ diff In y^2)=sqrt(6.25+25)=sqrt(31.25), so one-fifth of that added to sqrt(35), and the answer squared equals 45. That is going to be the sum of what is under the radical.
the equation of the line is y-y1=m(x-x1), m slope, and (x1, y1) a point.
the slope is -5/-2.5 or 2
y+2=2(x+3)
y=2x+4
graph the line
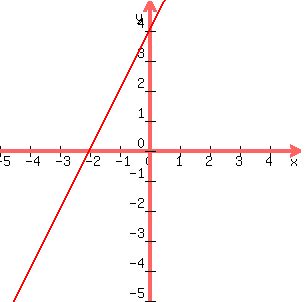
graph%28300%2C300%2C-5%2C5%2C-5%2C5%2C2x%2B4%29
The line is extended downward (closest to point A)
the distance is twice as much y as x
so the sqrt of( (5+2x)^2+(2.5+x)^2)=sqrt 45
so 25+20x+4x^2+6.25+5x+x^2=45
5x^2+25x-13.75=0
x^2+5x-2.75=0 or 4x^2+20x-11=0
(2x-1)(2x+11)=0
x=1/2, -5.5
Use the positive value. The other value would be the answer on the other end
The new end point is (-3.5, -3) and the new distance is sqrt(45), which is 1.2 * sqrt(31.25)