We must graph it and know some facts about the graph
and the equation of a parabola.
We plot the focus (a point) and the directrix (a line) in green:
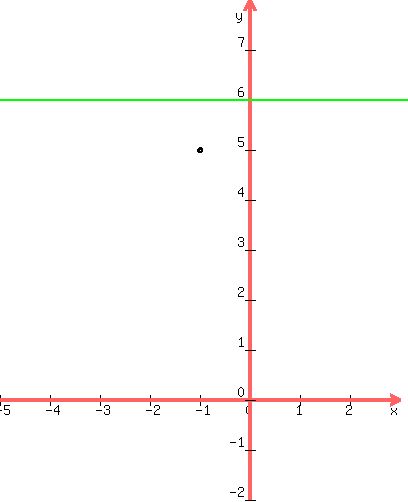We draw a line from the focus perpendicular to the directrix,
and find the midpoint.
The midpoint of that line is the vertex of the parabola.
We can tell from the graph that the vertex is (-1,5.5),
the vertex is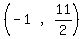 
Next draw two squares, one on each side of that line, with
that line as their common side:
Skwtch the parabola through the vertex and the left and right
bottom corners of those two squares:
The equation of a parabola that opens vertically is
Where the vertex is (h,k) =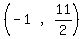
and p is the positive distance from the vertex to the focus,
so 
and if the parabola opens positive the sign is taken + and if
the parabola opens downward the sign is taken negative.
This parabola opens downward, so we use the - sign.
So the equation is:
which simplifies to:
Edwin
