|
Question 800737: Hi, I am preparing for an exam on Wednesday and this part of the problem of the pattern I seem to not get right.
the problem is about a growing pattern of bricks that are shaded and white bricks
t1 there are 3 shaded bricks
t2 there are 6 shaded bricks
t3 9 shaded bricks and 1 white one in the middle
t4 12 shaded bricks and 3 white bricks in the middle
the question posed:
Find the formula for the total number of bricks(shaded bricks and White bricks together) that you will need for the n-th wall
pattern shaded bricks: 3 ; 6 ; 9 ; 12 ; 15 ; 18 ; ... the formula is 3n
pattern white bricks 1 ; 3 ; 6 ; 10 ; ... the formula is n(n+2)/2
in the first term there is a difference of 3 and the second term the difference increases by one every time +2 ; +3 ; +4
I want to know do I add the two formula's I've tried everything, can you please help me.
Regards Olga
Found 2 solutions by rothauserc, KMST:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! first pattern is 3, 6, 9, 12, 15,18 and
the nth term is 3+(n-1)3
second pattern is 1, 3, 6, 10 and
the nth term is n(n+1)/2
we now add the two formulas
3+(n-1)3 + n(n+1)/2 = 3n + (n^2+n) /2 = (n^2 +7n) / 2
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  there are 3 shaded bricks there are 3 shaded bricks
 there are 6 shaded bricks there are 6 shaded bricks
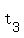 9 shaded bricks and 1 white one in the middle 9 shaded bricks and 1 white one in the middle
 12 shaded bricks and 3 white bricks in the middle 12 shaded bricks and 3 white bricks in the middle
The number of white bricks for 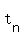 is zero for is zero for  and for and for 
The formula for the number of white bricks on wall number  should be should be 
 there are there are  white bricks white bricks
 there are there are  white bricks white bricks
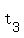 there are there are  white bricks white bricks
 there are there are  white bricks white bricks
For the next rows it would be  , ,  , ,  , and so on. , and so on.
So the sum (the total number of bricks on wall number  ) would be ) would be

Summarizing:

A further problem would be if the position of the white bricks in the wall matters. You do not say if there was a shape pattern, but I suspect I know what it was. I will add more as notes later, because it will take me a while to draw and explain.
NOTE 1:
I assume that your third wall look like this:
 Green outline brick means white brick, black outline means shaded brick. Green outline brick means white brick, black outline means shaded brick.
If your "walls" have pictures like that, read on.
Forget about algebra, about formulas, and about memorized recipes to solve problems of type this or that.
You probably have been encouraged to memorize and follow lots of formulas and problem solving recipes.
You probably have been encouraged to look at teachers for guidance and answers.
That is a very common, very sad, mid-crippling process that passes for education.
Asking the teacher (with a simpering smile) if this is "a plus problem", or if you have to multiply, or divide, will not help for this kind of exam.
We need more understanding, more independent thinking, less formulas, less reliance on someone else for answers.
Think like a fifth grader, or like a carpenter, or a gardener, with your own brain (and some basic stuff learned in elementary school).
Look at your "walls".
They are shaped like triangles.
The shaded bricks are all around the outside.
The white bricks (when there are any), are in the center.
When there are enough of those white bricks, they form a smaller triangle in the center of the triangular wall.
The number of total bricks, and the number of white bricks, are like the area of those triangles.
The number of shaded bricks is like the perimeter of the large triangle.
 That's intuition. Now we go for calculations. That's intuition. Now we go for calculations.
The first wall (wall number  ) has a bottom row of ) has a bottom row of  bricks, bricks,
and has a row of  bricks of top of that, bricks of top of that,
for a total of  rows, rows,
each row with one less brick than the one below.
The total number of bricks is a sum of 2 terms: 
Wall number  has a bottom row of has a bottom row of  bricks, bricks,
and each row of bricks has one less brick,
up to the top row, with just one brick,
for a total of  rows with a total of rows with a total of  bricks. bricks.
To find  we add the numbers of bricks for each of the we add the numbers of bricks for each of the  rows, from bottom row to top row, rows, from bottom row to top row,
  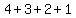 , or maybe we add top to bottom, and get , or maybe we add top to bottom, and get
  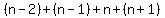
Adding those 2 equations together (pairing up terms), we get a sum of  pairs: pairs:
   so so
  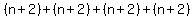
and since we are adding 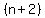 terms, for a total of terms, for a total of  terms, terms,
 --> -->  . .
Something like that goes for the white bricks, except that instead of starting with 2 rows,
with 2 bricks in the bottom row for row number 1,
and  bricks at the bottom in wall number bricks at the bottom in wall number  , ,
we start with 1 row of 1 white brick for wall number 3,
and have 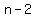 white bricks at the lowest of white bricks at the lowest of 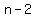 rows of white bricks in wall number rows of white bricks in wall number  , ,
for a total of  white bricks. white bricks.
The total number of shaded bricks in wall number  is just the number of bricks on the edge of a triangle with is just the number of bricks on the edge of a triangle with  bricks along each side. bricks along each side.
It is not  , because that would count each of the 3 corner bricks twice. It is , because that would count each of the 3 corner bricks twice. It is  less. It is less. It is  . .
NOTE 2:
A systematic approach to arithmetic sequences and series formulas:
School teaches about arithmetic sequences and their sums.
An arithmetic sequence is a sequence of numbers where there is a common difference between one number and the next.one.
We call the first term  , and the common difference , and the common difference  . .
From there we conclude that term number  , which we call , which we call  , ,
is related to  , and , and  by the equation/formula by the equation/formula
 . .
We can also deduce that the sum.  , of the terms from , of the terms from  to to  can be calculated as can be calculated as
 or or 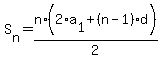
1) Given a mystery sequence, we want to see if it is an arithmetic sequence.
Is there is a common difference between one number to the next?
2) If the differences between consecutive terms of a sequence form an arithmetic sequence, we can use that to calculate a formula for the sequence.
1) If both of the approaches above fail, we may look further to see if it is a geometric sequence. We could try other approaches. Does a graph of the values remind us of some function we know? Is it is a Fibonacci sequence? What pattern could the person who wrote the problem be thinking of?
Back to your problem
Step 1)
3 ; 6 ; 9 ; 12 ; 15 ; 18 ; ... is an arithmetic sequence.
It's first term is 
The common difference is 
The formula for term number  for that arithmetic sequence is for that arithmetic sequence is

Step 2)
The sequences
0 ; 0 ; 1 ; 3 ; 6 ; 10 ; ... for the white bricks, and
3 ; 6 ; 10 ; 15 ; 21 ; 28 ; ... for the total number of bricks
are not arithmetic sequences.
However, the differences from one number to the next one in each sequence,
0 ; 1 ; 2 ; 3 ; 4 ; ... for the white bricks, and
and 3 ; 4 ; 5 ; 6 ; 7 ; ... for the total number of bricks
are arithmetic sequences.
To get to term number  of 3 ; 6 ; 10 ; 15 ; 21 ; 28 ; ... of 3 ; 6 ; 10 ; 15 ; 21 ; 28 ; ...
we can start with the first term,  and add the 5 differences between the first and 6th terms. and add the 5 differences between the first and 6th terms.
So 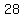 is is  plus the sum of the 5 terms plus the sum of the 5 terms 
of the arithmetic sequence 3 ; 4 ; 5 ; 6 ; 7 ; …
For the arithmetic 3 ; 4 ; 5 ; 6 ; 7 ; … .
 and and 
The sum of 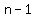 first terms of that sequence is first terms of that sequence is

Term number  of the sequence 3 ; 6 ; 10 ; 15 ; 21 ; 28 ; ... of the sequence 3 ; 6 ; 10 ; 15 ; 21 ; 28 ; ...
is that plus  , , 
The calculation for the sequence 0 ; 0 ; 1 ; 3 ; 6 ; 10 ; ... for the white bricks is similar.
The sum of the first 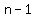 terms of the arithmetic sequence terms of the arithmetic sequence
0 ; 1 ; 2 ; 3 ; 4 ; ... is

Term number  of the sequence 0 ; 0 ; 1 ; 3 ; 6 ; 10 ; ... of the sequence 0 ; 0 ; 1 ; 3 ; 6 ; 10 ; ...
is that plus  , or , or 
|
|
|
| |