|
Question 1167049: The function f(x) is transformed to produce a function g(x) where g(x)=−2f(5x)−5. If (−9,4) is a point on the graph of f(x), give the coordinates of the transformed point on the graph if g(x).
Answer by ikleyn(52817)   (Show Source):
You can put this solution on YOUR website! .
The function f(x) is transformed to produce a function g(x) where g(x) = −2f(5x)−5.
If (−9,4) is a point on the graph of f(x), give the coordinates of the transformed point on the graph if g(x).
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The fact that (-9,4) is a point on the graph of f(x) means that
4 = f(-9).
Now, you need to have -9 = 5x, so for it you take x =  .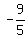
It provides you f(5x) = 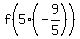 = f(-9) = 4. (1)
Next, according to the definition g(x) = -2f(5x) - 4,
you should multiply the '4' in (1) by (-2) and subtract 5 from the product.
It gives you the ordinate y = (-2)*4 - 5 = -8 - 5 = -13.
Thus the required point (x,y) is (, ).
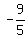This point is the transformed point on the graph of g(x).
At this point, the problem is solved completely.
-------------------------------
This problem is a standard/typical problem on analyzing points on transformed graphs,
and my solution is a standard reasoning to solve such problems.
|
|
|
| |
