|
Question 1164405: The functions f and g are defined as follows:
f(x) = sqrt(x+1/x-1) and g(x) = sqrt(x+1)/sqrt(x-1).
Explain why functions f and g are not the same function.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
These two functions, f(x) and g(x), have different domain;
in other words, they are defined in different sets of real numbers.
The domain for function g(x) is { x | x > 1 }.
The domain for function f(x) is the set of solutions to THIS inequality
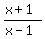 > 0,
which is the UNION of two sets
{ x < -1 } U { x > 1 },
where the numerator and denominator BOTH are negative OR BOTH are positive.
See this visual illustration, where I slightly changed function g(x) intently to make the difference visible.
Plot f(x) =  (red), g(x) = 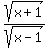 (green)
f(x) has two branches, as you see (two red lines);
g(x) has only one branch (only one green line).
Answered, solved and explained.
Is everything clear to you in my solution ?
`````````````````````````````````
If after reading my post you will have questions, do not hesitate to post them to me.
If you do, then please refer to the ID number of this problem, which is 1164405.
The ID number is the first number, which you see in your page in the UPPER LEFT corner.
If you will post to me without referring to this ID number, I will not know to whom to answer.
It is how this forum works.
So, mentioning this ID is NECESSARY, if you want to have two-way communication with me.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn answered the question you INTENDED to ask; and she answered it well.
On the other hand, answering the question you DID ask is trivial.
The functions
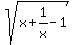
and
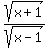
are not even remotely similar.
If you are asking a question on a topic like this, you should have enough knowledge of math to know that sometimes parentheses are required to show an expression correctly.
|
|
|
| |
