SOLUTION: You are selling banana bread that costs P 5 each. Each week, you have 50 customers. When you decrease the price by P1, you expect 30 customers to be added. What is the price of t

Click here to see ALL problems on Functions

Question 1098350: You are selling banana bread that costs P 5 each. Each week, you have 50
customers. When you decrease the price by P1, you expect 30 customers to be
added. What is the price of the banana bread that yields a maximum profit?
a. Analyze the problem.
b. What is the weekly sale if the cost of the banana bread is P5?
c. If the revenue (R) = number of bread x bread price. Write the equation of
the quadratic function given the situation above?
d. What is the price that yields the maximum revenue?
e. Find the maximum revenue.
Found 4 solutions by josgarithmetic, Theo, MathTherapy, ikleyn:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!

price customers 5 50 5-1 50+1*30 5-2 50+2*30 . . 5-n 50+30n n, decrease in price quantity

REVENUE:

PROFIT?
Weekly cost was given as THE banana bread, P 5.
Profit:

If you want to look for price which gives maximum revenue, then look for the maximum for , n being the price decrease from P 5.

Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website!
the formula for revenue is y = number of customers * price per customer.

you are given that you have 50 customers when the price is 5.

formula becomes y = 50 * 5

when you change the price by -1, you get 30 more customers.

let x represent the change in customers or price.

for every increase in x, the price goes up 1 and the number of customers goes down 30.

therefore, the equation for revenue becomes y = (50 - 30x) * (5 + x)

when x = 0, the revenue is 50 * 5 = 250
when x = -1, the revenue is 80 * 4 = 320
when x = -2, the revenue is 110 * 3 = 330
when x = -3, the revenue is 140 * 2 = 280
when x = -4, the revenue is 170 * 1 = 170
when x = -5, the revenue is 200 * 0 = 0

you can see that the maximum revenue is attained when x = -2.
at that point, the revenue is 330.

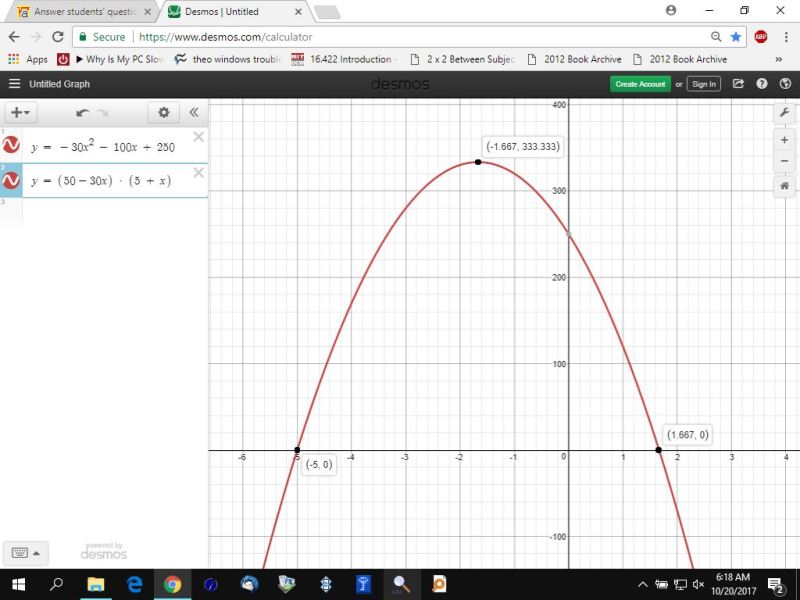
since this is a quadratic equation, the maximum revenue is found when x = -b/2a after you've placed the equation in standard format.

(50 - 30x) * (5 + x) is equal to 250 - 150x + 50x - 30x^2 which becomes 250 - 100x - 30x^2.

rearrange in descending order of degree, and the equation becomes -30x^2 - 100x + 250.

the maximum revenue is shown in the following graph, where the increments in the value of x are in whole units.

that maximum is attained when x = -2.
that represents 110 customer who pay 3 each for a total revenue of 330.

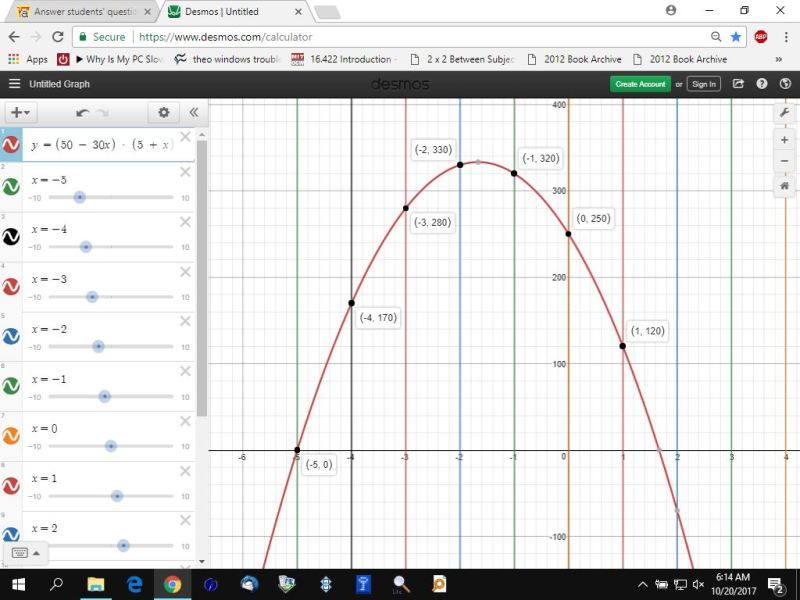
the theoretical maximum revenue is shown in the following graph, along with the zero crossing points that are achieved after factoring the quadratic equation.

Answer by MathTherapy(10552)   (Show Source):
You can put this solution on YOUR website!
You are selling banana bread that costs P 5 each. Each week, you have 50
customers. When you decrease the price by P1, you expect 30 customers to be
added. What is the price of the banana bread that yields a maximum profit?
a. Analyze the problem.
b. What is the weekly sale if the cost of the banana bread is P5?
c. If the revenue (R) = number of bread x bread price. Write the equation of
the quadratic function given the situation above?
d. What is the price that yields the maximum revenue?
e. Find the maximum revenue.

Weekly sale, at original price of P 5, and customer-count of 50:
With R being maximum revenue, and x, the number of PRICE REDUCTIONS, we get the following equation of the quadratic function:
Reduced price that yields maximum revenue:
Maximum revenue derived from reduced price of P 3.33, and increased customer-count, 100:

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

The formula for revenue is R(x) = (50+30x)*(5-x), where x = the price decrease from P5. R(x) = -30x^2 + 100x - x^2. The maximum of R(x) is achieved at x = = = 1.67 So, optimal decrease from P5 is P1.67, which means that the optimum price is P5 - P1.67 = P3.33. The maximal revenue is R(x) = (50+30*1.67)*(5-1.67) = P 333.33

Plot y = (50+30x)*(5-x), where x is the price deviation from P5