Question 1018321: Find the range of k for which the quadratic equation x^2-kx+3k-2=0 has two different solutions, one solution is within -1< x <0 an the other solution is within 1< x <2.
Let f(x)= x^2-kx+3k-2
Please show all working out. Thank you
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There may be a better way to get to the same answer.
Here is a cumbersome one.
Using the quadratic formula, we find that the solutions to  , ,
if any, are given by
 . .
For the solutions to exist, we need to have
 , and only if , and only if  there are two different solutions. there are two different solutions.
Since the solutions to  are are
 , ,
two different solutions to  exist only if exist only if
 or or 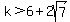 . .
If 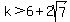 , ,  . .
So, if 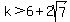 , there is one solution (the one above) that is , there is one solution (the one above) that is
neither within  nor within nor within  . .
If  , ,
and  is to have is to have
one solution within  , and , and
another solution within  , it must be , it must be
 , and , and  . .
 --> --> --> -->
Since 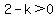 , ,
 --> --> --> --> --> --> --> --> --> --> --> -->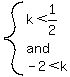 --> -->
 --> --> --> -->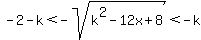 --> --> . .
As we already found out (above) that we need 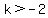 , , 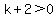 , so , so
 <--> <--> <--> <-->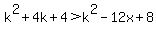 <--> <-->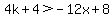 <--> <--> <--> <--> . .
In sum, the answer is  . .
|
|
|