Tutors Answer Your Questions about Finite-and-infinite-sets (FREE)
Question 1209457: List all subsets of {A,B,C,D}
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
List all subsets of {A,B,C,D}
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
It has one empty subset {}.
It has 4 (four) subsets consisting of one element.
These subsets are {A}, {B}, {C}, and {D}.
It has 6 (six) subsets consisting of two elements.
These subsets are {A,B}, {A,C}, {A,D}, {B,C}, {B,D}, {C,D}.
It has 4 (four) subsets consisting of three elements.
These subsets are {A,B,C}, {A,B,D}, {A,C,D}, {B,C,D}.
We obtain this list simply crossing out letter by letter from the list of 4 elements {A,B,C,D}.
Finally, the original set {A,B,C,D} has a unique subset {A,B,C,D}, which consists of 4 elements.
This subset is special: it is called "improper" subset.
Notice that the total number of subsets is 1 + 4 + 6 + 4 + 1 = 16 = 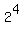 , ,
including empty subset and improper subset.
It is not a random coincidence and it is not accidently.
The general fact is that the number of all subsets of any finite set of "n" elements is  , ,
including empty subset and improper subset.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
A set is a collection of things. In this case letters A through D.
A subset is a smaller set that contains some of those letters.
It could be 0 of them, which gives the empty set. The empty set is a subset of every set.
It could be all of them. Any set is a subset of itself.
Or it could be something like {A,B,C} or {B,D}
To systematically list out every possible subset, we can use binary notation.
We count from 0 to (2^4)-1 = 15 in binary. The exponent 4 refers to the number of elements in the original set.
| Base10 | Base2 | | 0 | 0000 | | 1 | 0001 | | 2 | 0010 | | 3 | 0011 | | 4 | 0100 | | 5 | 0101 | | 6 | 0110 | | 7 | 0111 | | 8 | 1000 | | 9 | 1001 | | 10 | 1010 | | 11 | 1011 | | 12 | 1100 | | 13 | 1101 | | 14 | 1110 | | 15 | 1111 |
Counting in binary shouldn't be too tricky once you get a hang of it.
Basically you start at 0000 and increment the last digit by 1 to get 0001
Then increment the last digit of 0001 to get 0002, but the "2" doesn't exist in binary.
The only digits are 0 and 1.
A fundamental rule in binary is 12+12 = 102 or you can phrase it as saying "1+1 = 10 in binary".
This explains how we go from 0001 to 0010. The 1 carries over to the left.
Then we go from 0010 to 0011
Then from 0011 to 0100
And so on.
A recommended tool is to use the Dec2Bin spreadsheet function.
The first input of this function is the number we want to convert to binary. The second input is the number of digits for the output.
For example type in =Dec2Bin(A1,4) to convert whatever is in cell A1 to binary. It will have 4 binary digits.
There are many online calculators that can convert from decimal (base 10) to binary (base 2).
--------------------------------------------------------------------------------------------------
Why go through the trouble of using binary? Because 0 represents leaving out a particular letter while 1 represents including it.
String those 1's and/or 0's together to form a list of items.
0101 for instance means we exclude A, include B, exclude C, include D.
In short basically you have B and D to form the subset {B,D}
Another example is 1110 represents the subset {A,B,C} since we have 1's as the first three slots and 0 in the last slot.
As you can see this guarantees we do not overlook any subset.
Let's introduce a third column to the previous table that lists out all the subsets possible.
| Base10 | Base2 | Subset | | 0 | 0000 | { } | | 1 | 0001 | { D } | | 2 | 0010 | { C } | | 3 | 0011 | {C, D} | | 4 | 0100 | { B } | | 5 | 0101 | { B, D } | | 6 | 0110 | { B, C } | | 7 | 0111 | { B, C, D } | | 8 | 1000 | { A } | | 9 | 1001 | { A, D } | | 10 | 1010 | { A, C } | | 11 | 1011 | { A, C, D} | | 12 | 1100 | { A, B } | | 13 | 1101 | { A, B, D } | | 14 | 1110 | { A, B, C } | | 15 | 1111 | { A, B, C, D } |
Optionally we can sort the subsets like so
{ }
{ A }
{ B }
{ C }
{ D }
{ A, B }
{ A, C }
{ B, C }
{ A, D }
{ B, D }
{ C, D }
{ A, B, C }
{ A, B, D }
{ A, C, D }
{ B, C, D }
{ A, B, C, D }
Feel free to sort them any way you prefer.
{ } is the empty set. It has nothing inside it. Not even 0 is inside. The empty set is a subset of every set. Sometimes a special symbol is used for the empty set. The symbol looks like a zero with a slash through it.
The singletons are listed next. Singletons have 1 element as you can probably guess by the name. Then after the singletons are subsets with 2 elements. Then 3 element subsets and so on.
Since we have n = 4 slots and 2 choices per slot (either include the element or not), there are 2^n = 2^4 = 16 different subsets. The collection of all subsets is known as the Power Set.
Question 1208834: There are 7 books, 3 red, 2 blue, 1 orange. How many ways can these books be arranged on a shelf?
Thx!
Bernd
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are 7 books, 3 red, 2 blue, 1 orange. How many ways can these books be arranged on a shelf?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As I red the post, it seems to me that wording is incomplete.
A complete wording should connect arranging the books on the shelf with the colors of the books.
So, double check your post comparing with the source.
Question 1205854: Let U = {all soda pops},
A = {all diet soda pops},
B = {all cola soda pops},
C = {all soda pops in cans},and
D = {all caffeine-free soda pops}.
Describe the set in words.
A ∩ B
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! Describe the set in words.
A ∩ B
A ∩ B =>denotes the intersection of sets, which refers to elements that are common to all the sets being considered
in your case refers to all soda pops that are simultaneously diet and cola
A ∩ B={all diet and cola soda pops}
Question 1205773: Mr. Thompson wants to make monthly deposits into an annuity for his child so that $10,000 will be available in 8 years. If the interest rate is 8% compounded monthly, find the full deposit.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Mr. Thompson wants to make monthly deposits into an annuity for his child
so that $10,000 will be available in 8 years.
If the interest rate is 8% compounded monthly, find the full deposit.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
If the monthly deposits are made at the end of each month, then it is a classic
Ordinary Annuity saving plan. The general formula is
FV =  ,
where FV is the future value of the account; P is the monthly payment (deposit);
r is the monthly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P = ,
where FV is the future value of the account; P is the monthly payment (deposit);
r is the monthly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P =  . (1)
Under the given conditions, FV = $10,000; r = 0.08/12; n = 8*12 = 96.
So, according to the formula (1), you get for the monthly payment
P = . (1)
Under the given conditions, FV = $10,000; r = 0.08/12; n = 8*12 = 96.
So, according to the formula (1), you get for the monthly payment
P = 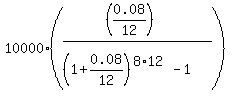 = $74.70.
Answer. The necessary monthly deposit value is $74.70.
Note that of projected $10,000, the total of the deposits will be only 8*12 times $74.70,
i.e. 8*12*74.70 = 7171.20 dollars. The rest is what the account will earn/accumulate in 8 years. = $74.70.
Answer. The necessary monthly deposit value is $74.70.
Note that of projected $10,000, the total of the deposits will be only 8*12 times $74.70,
i.e. 8*12*74.70 = 7171.20 dollars. The rest is what the account will earn/accumulate in 8 years.
---------
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
/////////////////////
To make such complicated calculations as they are in this problem,
you should have/use an appropriate calculator for such long formulas.
Ideal choice is MS Excel, if you have it in your computer.
Then you write a formula in a text editor, copy-paste it
into an Excel work-sheet cell and click "enter" - the result is ready
instantaneously.
If you have no MS Excel in your computer, you may find similar
free of charge calculators in the Internet. One such calculator is
www.desmos.com/calculator
It allows you to do the same thing: you write a formula in a text editor,
copy-paste it into this calculator and click "enter" - the result is ready
instantaneously.
Question 1201448: Let A and B be subsets of a universal set U and suppose n(U) = 200, n(A) = 100, n(B) = 80, and n(A ∩ B) = 40. Compute:
n(A ∪ B)
n(Ac)
n(A ∩ Bc)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let A and B be subsets of a universal set U and suppose n(U) = 200, n(A) = 100, n(B) = 80, and n(A ∩ B) = 40. Compute:
(a) n(A ∪ B)
(b) n(Ac)
(c) n(A ∩ Bc)
~~~~~~~~~~~~~~~~~~~~
(a) n(A U B) = n(A) + n(B) - n(A ∩ B) = 100 + 80 - 40 = 140.
(b) n(A^c) = n(U) - n(A) = 200 - 100 = 100.
(c) The set A ∩ B^c consists of those elements from A that do not belong to B.
In other words, A ∩ Bc = A \ (A ∩ B).
THEREFORE, n(A ∩ B^c) = n(A) - n(A ∩ B) = 100 - 40 = 60.
Solved.
I answered all your questions.
Question 1201171: 1. P ⊃ (G ⊃ T) 2. Q ⊃ (T ⊃ E) 3. P 4. Q / G ⊃ E
1. ∼S ⊃ D 2. ∼S ∨ (∼D ⊃ K) 3. ∼D / K
1. N ⊃ (J ⊃ P) 2. (J ⊃ P) ⊃ (N ⊃ J) 3. N / P
Need these three problems solved with rules of inference.
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
First problem
-------------
1. P-->(G-->T) Premise
2. Q-->(T-->E) Premise
3. P Premise
4. Q Premise
// show G-->E
5. G-->T 3,1 Modus Ponens (MP)
6. T-->E 4,2 MP
7. G-->E 5,6 Hypothetical Syllogism (HS)
*** done ***
Second problem (Learn from the other two solutions, and you should
be able to easily fill in steps 4 and 5).
-----------------------------------------
1. ~S-->D Premise
2. ~Sv(~D-->K) Premise
3. ~D Premise
// show K
4. 3,1 Modus Tollens (MT)
5. 4,2 Disjunctive Syllogism (DS)
6. K 3,5 Modus Ponens (MP)
*** done ***
Third problem
-------------
1. N-->(J-->P) Premise
2. (J-->P)-->(N-->J) Premise
3. N Premise
// show P
4. J-->P 3,1 Modus Ponens (MP)
5. N-->J 4,2 MP
6. J 3,5 MP
7. P 6,4 MP
*** done ***
If you have questions, send via the 'thank you' form.
Question 1197905: If the universal set U = {1,2,3,4 5,6,7,8,9} and if set A = {1,3,5,7,9}, find the complement of set A.
Let me see.
Let A_c = complement of set A
A_c = {2,4,6,8}.
It follows from the definition of complement that set A united with A_c = set U.
Question:
Why does set A intersected with A_c = empty set?
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1197897: Given that set E = {x | x is an even digit }, use the Roster Method to show the even digits requested.
According to the textbook author, the answer is E = {0, 2, 4, 6, 8}.
My question is about 0. Is zero an even digit? Why is 0 on that list of even digits for set E?
Found 2 solutions by math_helper, math_tutor2020:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! An even number is a number which when divided by 2, leaves no remainder.
0 / 2 = 0 (no remainder, so zero is even since it passes the zero remainder test)
On a related note about zero (0): zero is neither negative nor positive. So when a problem says something like 'x is a positive number' you are dealing with a number that is strictly greater than zero. When the author wishes to include zero, you might see wording such as 'x is a nonnegative number...'.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
An even number is anything that is a multiple of 2.
More formally, it's a number of the form 2k where k is an integer.
set of integers = {..., -3, -2, -1, 0, 1, 2, 3, ...}
i.e. set of positive and negative whole numbers, with 0 thrown in as well.
If k = 5 for instance, then 2k = 2*5 = 10 which is even.
Or if k = 27, then 2k = 2*27 = 54 which is also even.
We can show that 0 is even since,
2k = 0
k = 0/2
k = 0
So 2k = 2*0 = 0 is an even number.
Further Reading
https://mathworld.wolfram.com/EvenNumber.html
Question 1185955: Find the payment that should be used for the annuity due whose future value is given. Assume that the compounding period is the same as the payment period.
$20,000; quarterly payments for 17 years; interest rate 5%
the payment should be? $
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the payment that should be used for the annuity due whose future value is given.
Assume that the compounding period is the same as the payment period.
$20,000; quarterly payments for 17 years; interest rate 5% the payment should be?
~~~~~~~~~~~~~~~~~~~
What @Theo calculated for you, was the Ordinary Annuity saving plan, when the regular deposits are made at the END of each quarter.
The given problem asks about the Annuity Due saving plan, when the regular deposits are made AT THE BEGINNING of each quarter.
So, @Theo's calculations are not appropriate for this problem.
THEREFORE, I came to bring you a correct solution.
It is a classic Annuity Due saving plan. The general formula is
FV = 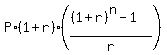 , (1)
where FV is the future value of the account; P is your quarterly payment (deposit), which is made at the beginning of each quarter;
r is the effective quarterly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 4, in this case).
Under the given conditions, FV = 20000; r = 0.05/4; n = 17*4 = 68. So, according to the formula (1), the quarterly payment should be
P = , (1)
where FV is the future value of the account; P is your quarterly payment (deposit), which is made at the beginning of each quarter;
r is the effective quarterly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 4, in this case).
Under the given conditions, FV = 20000; r = 0.05/4; n = 17*4 = 68. So, according to the formula (1), the quarterly payment should be
P = 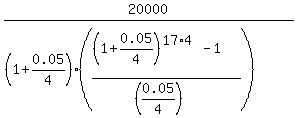 = $186.02. ANSWER
Note that you deposit only 17*4*$186.02 = $12,649.36. The rest is what the account earns/accumulates in 17 years. = $186.02. ANSWER
Note that you deposit only 17*4*$186.02 = $12,649.36. The rest is what the account earns/accumulates in 17 years.
-----------------
On Ordinary Annuity and Annuity Due saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
Answer by Theo(13342)   (Show Source): (Show Source):
Question 1180845: How will this expression be in sigma notation
5/2x^3 + 3x^4 + 7/2x^5 + 4x^6
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From my point of view, BOTH the posed question/problem and the answer in the post by @MathLover1
are nonsensical to such a degree, that BOTH DO NOT DESERVE any discussion.
Both are good for recycling, ONLY.
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1177776: A particular fruit's weights are normally distributed, with a mean of 541 grams and a standard deviation of 22 grams.
If you pick one fruit at random, what is the probability that it will weigh between 572 grams and 597 grams
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
Normal Distribution: μ = 541 σ = 12
Using TI or similarly an inexpensive calculator like a Casio fx-115 ES plus
P(572< x < 597) = normalcdf( 572, 597, 541, 12) = .0049
Important You feel comfortable with Your Calculator.
Wish You the Best in your Studies.
Question 1177775: According to a recent survey, 90% of students say that they do not get enough sleep. Assume the survey meets the conditions of a binomial experiment. Round your answers to three decimal places
In a random survey of 28 students, find the probability that exactly 26 of them will say that they do not get enough sleep:
In a random survey of 28 students, find the probability that more than 26 of them will say that they do not get enough sleep:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
Binomial Distribution: p(do not get enough sleep) = .9
Using TI or similarly an inexpensive calculator like a Casio fx-115 ES plus
n = 28
... P(x = 26) = binompdf(28, .9, 26) = .2442
... P(x > 26) = 1- P(x ≤ 26)= 1 - binomcdf(28, .9, 26) = 1-.7848 = .2152
Important You are comfortable using Your Calculator.
Wish You the Best in your Studies.
Question 1173190: Let G ={4x | x ∈ N} H ={y | y is a prime number}
Find G ∩ H.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: The empty set
We can denote this as { } which is just a pair of curly braces with nothing inside it. We could also use the special symbol  to denote the empty set. to denote the empty set.
---------------------------------------------------
Explanation:
Set G describes all multiples of 4. So we have: {4,8,12,16,...}
Set H describes the set of prime numbers: {2,3,5,7,11,...}
The two sets have nothing in common.
Any multiple of 4 will have 4 as a factor. The value 4 itself isn't prime. A prime number only has factors of 1 and itself. For instance, 7 is prime because the only factors of it are 1 and 7.
So this is why if you select a multiple of 4, then it won't be prime. If you select a prime number, then it won't be a multiple of 4.
Because the two sets have nothing in common, their intersection is the empty set.
Question 1167127: Consider the finite number of sets A1= (−1,1), A2= [1,10), A3= [−10,−1], A4= [10,∞), and A5= (−∞,−10). Prove or disprove that there is a partitionof real numbers for the collection {A1, A2, A3, A4, A5}.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The five sets together exactly cover the whole number line without overlap, so they form a partition of the real numbers.
A5: -infinity to -10, not including -10
A3: -10 to -1, including both endpoints
A1: -1 to 1, including neither endpoint
A2: 1 to 10, including 1 but not 10
A4: 10 to infinity, including 10
Question 1166782: I just need help with letter C and please do a step by step explanation.
A group of 8 workers decides to send a delegation of 4 to their supervisor to discuss their grievances. Complete parts (a) through (c) below.
A) How many delegations are possible?
B) If it is decided that a particular worker must be in the delegation, how many different delegations are possible?
C) If there are 3 women and 5 men in the group, how many delegations would include at least 1 woman?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I just need help with letter C and please do a step by step explanation.
A group of 8 workers decides to send a delegation of 4 to their supervisor to discuss their grievances.
Complete parts (a) through (c) below.
A) How many delegations are possible?
B) If it is decided that a particular worker must be in the delegation, how many different delegations are possible?
C) If there are 3 women and 5 men in the group, how many delegations would include at least 1 woman?
~~~~~~~~~~~~
In my post, I will answer parts A) and B) only.
(A) Each delegation is a subset of 4 elements of the whole set of 8 workers.
Such subsets can be chosen by different ways.
These subsets are called combinations.
If you have a set of "n" elements and select the subsets consisting of "k" elements,
then these subsets are calling "combinations of n items taken k at a time".
The number of such subsets (=such combinations) is denoted 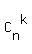 , and
there is a formula to calculate , and
there is a formula to calculate 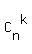 . This formula is . This formula is
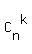 = = 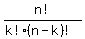 = = 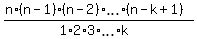 .
In particular, in your case (A), the number of possible delegations is .
In particular, in your case (A), the number of possible delegations is
 = = 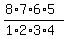 = 7*2*5 = 70.
So, the answer to part (A) is 70: 70 different delegations are possible.
Part (A) is COMPLETED.
(B) If it is decided that one particular worker must be in the delegation, then we choose only 3 remaining
members of delegation among 8-1 = 7 remaining workers.
It is = 7*2*5 = 70.
So, the answer to part (A) is 70: 70 different delegations are possible.
Part (A) is COMPLETED.
(B) If it is decided that one particular worker must be in the delegation, then we choose only 3 remaining
members of delegation among 8-1 = 7 remaining workers.
It is  different combinations, and different combinations, and  = = 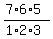 = 7*5 = 35.
It is the answer to part (B) = 7*5 = 35.
It is the answer to part (B)
------------
At this point I will stop my explanations.
Usually, students learn this knowledge from schools, from school teachers and from their textbooks.
Usually, it is not our profile at this forum to teach from scratch: as a rule, we assume that the students /(the visitors)
come to the forum just having some basic knowledge.
But in any case, from this my post you may learn these basics.
This subject, called "COMBINATIONS", can not be learned momentarily, at one instance.
It requires gradual submersion.
In this site, there are lessons devoted to this subject, so you have a unique and happy opportunity to learn from these lessons.
These introductory lessons are
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- OVERVIEW of lessons on Permutations and Combinations
You even may find typical solved problems there, similar to your problem.
After reading and first submersion to the subject, you may come again to the forum with the next portion of your problems and questions.
Happy learning (!)
Question 1166087: Let S be the universal set, where:
S={1,2,3,...,18,19,20)
Let sets A and B be subsets of S, where:
Set A= {2,4,5,11,13,14,15,16,19}
Set B= {2,5,7,9,10,11,14,15,17,18,20}
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1165706: enter any no. = 5
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I zeroed this post and re-directed it to the trash bin due to absence of any sense in it.
I did it with the educational purpose to teach you do not post nonsense to this forum.
But, from the global point of view, it does not matter to me, if you are able to learn or not.
What really matters to me is DO NOT HAVE nonsensical posts at this forum.
Question 1164947: In a potato race, 10 potatoes are placed in a straight line 5 meters apart, the first potato being placed 6 meters from the starting point. how many meters does a contestant travel in collecting the potatoes one at a time and placing them in a basket located at the starting point
Found 2 solutions by Boreal, htmentor:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! It is a series with the first term 6 m out and back or 12 m
the second term is 11 m out and back or 22 m
and so forth until the n th term is (6+5(n-1)) out and back or 12+10n-10 m or 10n +2
The last term will be 102 m with n=10
so the series is 12+22+32+...+102
a1=12
a10=102
sum is (n/2)(a1+an)
=5(12+102)
=570 m
can check
12+22+32+42+52+62+72+82+92+102
Answer by htmentor(1343)   (Show Source): (Show Source):
You can put this solution on YOUR website! The distance travelled to retrieve each potato will be twice the distance from the starting point to the potato.
The first distance will be 12 m since the first potato is located 6 m from the starting point
In general, the distance travelled to retrieve the n-th potato is represented by an arithmetic sequence,
with the first term equal to 12. The common difference is 10, twice the distance between each potato.
Thus a_n = 12 + 10(n-1)
The sum of 10 terms of the arithmetic sequence S_n = (10/2)*(12 + 102) = 570 m
Question 1157270: Paradise river cruises operates a fleet of river vessels. The fleet has two types of vessels: A type A vessel has 60 deluxe cabins and 160 standard cabins, whereas a type B vessel has 80 deluxe cabins and 120 standard cabins. Under a charter agreement with odyssey travel agency, paradise river cruises is to provide odyssey with a minimum of 460 deluxe and 780 standard cabins for their 2 week cruise in may. It costs $58,000 to operate a type A vessel and $75,000 to operate a type B vessel for that period. How many of each type vessel should be used to keep operating costs to a minimum?
A.Set up table to represent this information
B. (Be specific) let variable x represent
(Be specific) let variable y represent
C. Write the objective function and whether it is to be minimized or maximized
D. Write the constraints
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let x equal the number of type A vessels.
let y equal the number of type B vessels.
your objective function is:
58000 * x + 75000 * y
this is the cost you want to minimize.
your constraints are:
60x + 80y >= 460
this is the number of deluxe cabins you need to supply a minimum of.
160x + 120y >= 780
this is the number of standard cabins you need to supply a minimum of.
x >= 0
y >= 0
this tells you that the number of cabins can't be negative.
Question 1154055: -39, -44, -49, -54, ...
Find a35
Found 2 solutions by jim_thompson5910, ikleyn:
Answer by jim_thompson5910(35256)  (Show Source): (Show Source):
You can put this solution on YOUR website!
There are 2 ways to do this kind of problem.
The first method involves listing out 35 terms, each new term is found by subtracting 5 from the previous term (eg: -39 - 5 = -44, or -44-5 = -49, and so on). This is not recommended because there are so many terms. It's easy to lose track.
A much better method is to use the general nth term formula of an arithmetic sequence. That formula is

The first term is  . The common difference is . The common difference is  since we add on -5 each time, or subtract 5 each time, to get the next term. since we add on -5 each time, or subtract 5 each time, to get the next term.
So,




--------------------------------------------------------
As a check, let's plug in a random positive integer between 1 and 4 to see if it matches up with the proper element in the sequence we're given. I'll do n = 3

 Replace n with 3 Replace n with 3


The third term is -49
Sure enough, the third term of the given sequence {-39, -44, -49, -54, ...} is -49. I'll let you check the other values of n (1, 2 and 4) to see if things line up properly or not.
--------------------------------------------------------
Once we know the nth term formula, we plug in n = 35 to get the 35th term of the arithmetic sequence

 Replace n with 35 Replace n with 35


The 35th term is -209
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1153949: calculate the number of subsets and proper subsets for each set.
{x|x Є N and 0 < x ≤ 4}
{x|x is the number of sides on a pentagon}
Thank you in advance,
SYL
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I will give the solution for the first set, where the meaning is clear.
The set contains 4 integer numbers 1,2,3,4.
Hence, the number of all subsets is 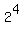 = 16.
Exclusing one improper subset, you obtain 16-1 = 15 proper subsets. ANSWER = 16.
Exclusing one improper subset, you obtain 16-1 = 15 proper subsets. ANSWER
See the lesson
- Counting elements in sub-sets of a given finite set
in this site.
/\/\/\/\/\/\/\/
For the second "set", the meaning is dark, so I even will not touch it.
Question 1153012: What is The next number in the sequence 3, 2, 6, 4, 9, 6, 12, 8
Answer by MathIsHard_Yay(7)  (Show Source): (Show Source):
You can put this solution on YOUR website! Ok. Okay.
Here's the pattern.
-1, +4
-2 +5
-3 +6
-4, And the one where it leaves you off on.
According to the pattern, you should add 7, giving you a final answer of 15.
Question 1149458: Define Periodic semigroup? Give three examples of periodic semigroup.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Please stop posting about semigroups.
Thank you VERY much.
-------------
Comment from student : I AM NOT SATISFIED WITH THIS ANSWER.
I DID NOT GET ANY EXAMPLE. I AM NOT HAPPY WITH THIS.
-------------
My response : Your posts about semigroups are out of the profile of this forum.
Actually, with my posts I saved your time from submitting many other similar posts from your side
and from useless waiting for responses.
Also, in my posts I was EXTREMELY POLITE with you.
Therefore, you should be thankful to me very much (!)
--------------
Comment from student: OKAY THANKS FOR REPLY. WHAT IS WEBSITE WHERE I GET SOLUTIONS OF SEMIGROUP QUESTIONS.
IF YOU KNOW PLEASE ANSWER.
Comment from student: madam do you know any link where we can solutions and examples of semigroups and its types.
--------------
My response
https://www.ams.org/books/surv/007.1/surv007.1-endmatter.pdf
http://www-groups.mcs.st-andrews.ac.uk/~alanc/pub/c_semigroups/c_semigroups_a4.pdf
http://math.uga.edu/~pete/semigroup.pdf
https://www.math.unl.edu/~jmeakin2/groups%20and%20semigroups.pdf
Question 1149481: Solve Research Paper "NOTE ON EXCLUSIVE SEMIGROUPS" by Miyuki Yamada.
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1149263: Prove that field has no proper ideal?
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1148462: Mr. Nakamura wants to make monthly deposits into an annuity for his grandchild so that $10,000 will be available in 6 years. If the interest rate is 9% compounded monthly, find the monthly deposit. (Round your final answer to two decimal places.)
Found 2 solutions by MathTherapy, ikleyn:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Mr. Nakamura wants to make monthly deposits into an annuity for his grandchild so that $10,000 will be available in 6 years. If the interest rate is 9% compounded monthly, find the monthly deposit. (Round your final answer to two decimal places.)
IKLEYN made a mistake.
A monthly payment of $51.68 would be enough for TEN (10) years, which is what she calculated.
However, a monthly payment of $105.26 would be enough for SIX (6) years, which is what is needed.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Thanks to @MathTherapy, who noticed my fault.
I re-edited / re-calculated my post, and a renewed / corrected version is below.
It is a classic Ordinary Annuity saving plan. The general formula is
FV =  ,
where FV is the future value of the account; P is the monthly payment (deposit); r is the monthly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P = ,
where FV is the future value of the account; P is the monthly payment (deposit); r is the monthly percentage yield presented as a decimal;
n is the number of deposits (= the number of years multiplied by 12, in this case).
From this formula, you get for the monthly payment
P =  . (1)
Under the given conditions, FV = $10,000; r = 0.09/12; n = 6*12. So, according to the formula (1), you get for the monthly payment
P = . (1)
Under the given conditions, FV = $10,000; r = 0.09/12; n = 6*12. So, according to the formula (1), you get for the monthly payment
P = 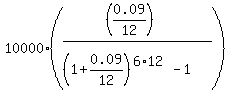 = $105.26.
Answer. The necessary monthly deposit value is $105.26. = $105.26.
Answer. The necessary monthly deposit value is $105.26.
---------
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
Question 1148489: A 12-year-old child received an inheritance of $3000 per year. This was to be invested and allowed to accumulate until the child reached 21 years of age. The first payment was made on the child's 12th birthday and the last on the 21st birthday. If the money was invested at 5.5% compounded annually, what did the child receive at age 21? (Round your final answer to two decimal places.)
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is a classic Ordinary Annuity saving plan. The general formula is
FV =  , (1)
where FV is the future value of the account; P is your annual payment (deposit); r is the annual percentage rate presented as a decimal;
n is the number of deposits (= the number of years, in this case).
Under the given conditions, P = 3000; r = 0.055; n = 10 (the number of the 3000 deposits).
So, according to the formula (1), you get at the 21-th birthday
FV = , (1)
where FV is the future value of the account; P is your annual payment (deposit); r is the annual percentage rate presented as a decimal;
n is the number of deposits (= the number of years, in this case).
Under the given conditions, P = 3000; r = 0.055; n = 10 (the number of the 3000 deposits).
So, according to the formula (1), you get at the 21-th birthday
FV =  = $38626.06. ANSWER = $38626.06. ANSWER
-----------------
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
Question 1148486: A man borrowed $950. Six months later, he repaid the loan (principal and interest) with $1150. What simple interest rate did he pay? (Round your final answer to two decimal places.)
Found 2 solutions by josmiceli, ikleyn:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1150 = 950 + 950*r*0.5
1150-950 = 950*r*0.5
200 = 950*r*0.5
r = 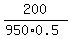 = 0.421 = 42.1% annual percentage rate simple interest (aproximately). = 0.421 = 42.1% annual percentage rate simple interest (aproximately).
In my solution, 0.5 = 0.5 of an year = 6 months.
Question 1148484: Alex expects to graduate in 3.5 years and hopes to buy a new car then. He will need a 20% down payment, which amounts to $3600 for the car he wants. How much should he save now to have $3600 when he graduates if he can invest it at 6% compounded monthly? (Round your final answer to two decimal places.)
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1148463: The Martinelli family sells some property obtained from an inheritance. How much should they invest at 7% compounded annually in order to have $23,000 in 6 years? (Round your final answer to two decimal places.)
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In a year with 7% annual interest, the value of an investment grows by a factor of 1+.07 = 1.07.
In t years the value grows by a factor of (1.07)^t.
You want the value of initial amount x to be $23,000 after 6 years:


Use a calculator....
Question 1143220: Show that the following sets have the same cardinality:
Integers divisible by 3 and even positive integers.
Thank you in advance for the help!
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I won't do the proof for you but I'll help you get the idea of how
to do it.
It may be enough to tell you that every positive even integer is
either of the form 4n+4 or -4n+2, for some integer -- if not, maybe
this discussion will help:
Make these sequences and correspondences between them. Notice how
they're split into sub-sequences left right and middle. Notice their
respective nth terms. We let 0 of the top sequence correspond to
0 of the multiples of 3 and to 2 of the positive multiples of 2.
{n} ..., -3, -2, -1, 0, 1, 2, 3, ... {n}
||| | | | | | | | |||
{3n} ..., -9, -6, -3, 0, 3, 6, 9, ... {3n}
||| | | | | | | | |||
{-4n+2} ..., 14, 10, 6, 2, 4, 8, 12, ... {4n+4}
The top sequence is the sequence of integers
The middle sequence is the sequence of integers divisible by 3.
The bottom sequence are the even positive integers, but they're
written according to this pattern:
We put 2 in the middle (corresponding to 0), then 4 on the right
of 2, then 6 on the left of 2, then 8 on the right of 4, then 10
on the left of 6, etc.
The sequence on the bottom right has nth term 4n+4, whereas the
sequence on the left has nth term -4n+2. Every positive even
integer is either of the form 4n+4 or -4n+2, for some integer.
You now show that the mapping is a bijection (into and onto).
Now you have enough equipment to write up a proof.
Edwin
Question 1142878: How many numbers 1 to 50 inclusive, have a perfect square as a factor?
Answer by solver91311(24713)   (Show Source): (Show Source):
Question 1135349:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1132653: Hi,
I cannot figure out the final number in the below sequence, and the associated rule.
546,548,563,556,580,564,?
Thanks!
Fay
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1131680: Find the discount D and the amount the borrower receives (proceeds) PR for the discount loan.
M = $960, d = 6.25%, t = 10 months
D = $
PR = $
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1131657: Brooks Bros. Company purchased a piece of equipment and used the straight-line depreciation method. The company books showed that the book value was $14,475 at the end of the third year and $8275 at the end of the seventh year.
(a) Find the linear equation B(x) relating book value and number of years.
B(x) =
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! these are ordered pairs (3, 14475) and (7, 8275)
the slope is -6200/4=-1550
point-slope formula y-y1=m(x-x1) m slope and (x1, y1) point
y-8275=-1550(x-7)
y=-1550x+10850+8275
B(x)=-1550x+19125 ANSWER

|
|