Question 979038: I have work for this question but i couldn't get the proper answer, please help me solve it.
Multiply 11321*12 base 4
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Base 4 arithmetic is easier than base 10 arithmetic,
because there are less "math facts" that your elementary teachers would make you memorize.
Some are just like for base 10 arithmetic:











Some other "math facts" look weird, different.
However, you do not need to memorize them,
because you have already memorized more than enough.
Just remember that
when you would write a number in base 10 with a digit other that 0, 1, 2, or 3,
the same number would look different in base 4.
The number after 3 is written as 4 in base 10,
but you write it as 10 in base 4.
The number after that is written at 5 in base 10,
but you write it as 11 in base 4.
And so on, so the counting numbers in base 4 are:
1, 2, 3, 10, 11, 12, 13, 100, 101, 102, 103, 110, 111, 112, 113, 120, 121, ...
So the strange math facts are:





 . .
Other than that, you use the same algorithms (procedures) for adding and multiplying.
You work with columns and "carry the 1" the same way, for example.
To multiply 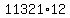 you start by multiplying you start by multiplying  . .
(It turns out that in base 4,  ) . ) .
Then you multiply 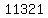 times the times the  from from  . .
(It is  , as it would be for base 10). , as it would be for base 10).
You write that with a  at the end, at the end,
as 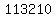 , ,
right below 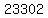 , ,
and you add them, carrying the 1's as needed.
. 23302
+113210
--------
203112 , because
when you add 3+2=11 for the third digit from the right,
you write 1 and carry the other 1;
when you add  for the fourth digit from the right, for the fourth digit from the right,
you still have to add the 1 carried over to get  , ,
and you have to write 3 as the fourth digit from the right,
and carry the 1,
and for the fifth digit from the right,
 , ,
but when you add the 1 carried over  , ,
and you have to write the  as the fifth digit from the right, as the fifth digit from the right,
and carry the 1.
It turns out that in base 4, 
The far right digit (the ones digit) is  . .
The digit to the left of that comes from  , ,
so that is a  , and you "carry the 1". , and you "carry the 1".
The digit to the left of that (the third digit from the right) comes from  , ,
but you also have to add the  carried over, carried over,
so you have  , ,
so you write the  } as the third digit from the right, } as the third digit from the right,
and "carry the 1".
The fourth digit from the right) comes from  , ,
but you also have to add the  carried over, carried over,
so you have  , ,
so you write the  as the fourth digit from the right. as the fourth digit from the right.
The fifth digit from the right) comes from  , ,
and since you have nothing carried over,
you just write the  as the fifth digit from the right. as the fifth digit from the right.
|
|
|