SOLUTION: A stream of water in steady flow from a kitchen faucet. At the faucet the diameter of stream is 0.96 cm. The stream fills a 125 cm^3 in 16.3 seconds. Find the diameter of the strea

Algebra ->  Finance -> SOLUTION: A stream of water in steady flow from a kitchen faucet. At the faucet the diameter of stream is 0.96 cm. The stream fills a 125 cm^3 in 16.3 seconds. Find the diameter of the strea      Log On


   

Question 885774: A stream of water in steady flow from a kitchen faucet. At the faucet the diameter of stream is 0.96 cm. The stream fills a 125 cm^3 in 16.3 seconds. Find the diameter of the stream 13 cm below the opening of the faucet.
Found 2 solutions by Alan3354, KMST:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
A stream of water in steady flow from a kitchen faucet. At the faucet the diameter of stream is 0.96 cm. The stream fills a 125 cm^3 in 16.3 seconds. Find the diameter of the stream 13 cm below the opening of the faucet.
-------------
Find the speed of the stream at the faucet:
Flow rate = Vol/sec = area*speed = 125/16.3 cc/sec
area*speed = 125/16.3
area+=+pi%2Ar%5E2+=+0.48%5E2%2Api+=+0.2304pi (area at the faucet)
speed+=+%28125%2F16.3%29%2F%280.2304pi%29
speed =~ 10.595 cm/sec (speed at the faucet)
------
Use h%28t%29+=+-4.9t%5E2+-+10.595t to find the time it takes to fall 13 cm
13 cm = 0.13 meters
h%28t%29+=+-4.9t%5E2+-+10.595t+=+-0.13
-4.9t%5E2+-+10.595t+%2B+0.13+=+0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case -4.9x%5E2%2B-10.595x%2B0.13+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-10.595%29%5E2-4%2A-4.9%2A0.13=114.802025.

Discriminant d=114.802025 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--10.595%2B-sqrt%28+114.802025+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-10.595%29%2Bsqrt%28+114.802025+%29%29%2F2%5C-4.9+=+-2.17444598843739
x%5B2%5D+=+%28-%28-10.595%29-sqrt%28+114.802025+%29%29%2F2%5C-4.9+=+0.0122010904782066

Quadratic expression -4.9x%5E2%2B-10.595x%2B0.13 can be factored:
-4.9x%5E2%2B-10.595x%2B0.13+=+%28x--2.17444598843739%29%2A%28x-0.0122010904782066%29
Again, the answer is: -2.17444598843739, 0.0122010904782066. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+-4.9%2Ax%5E2%2B-10.595%2Ax%2B0.13+%29

====================
t = 0.0122 seconds
The water is accelerated at 9.8m/sec/sec
Its speed after 0.0122 seconds is 0.10595 m/sec + 9.8*0.0122
= 0.22551 m/sec
= 22.551 cm/sec
-------------
Area at that speed = (125/16.3)/22.551 sq cm
Area =~ 0.3400608 sq cm = pi*r^2
r = 0.329 cm
d = 0.658 cm
=======================
So you have 2 answers that don't agree.
You can see how it's done.
Check the work, pick the one you like.

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Disclaimer/apology:
I apologize to you in advance for possible mistakes. I try to keep all my units straight, and calculate correctly, but I am prone to punching in the wrong numbers in the computer and calculator/
I also apologize to professor Walter Lewin.
My grasp of physics was never strong enough for my taste, even after paying attention at some (though not all) of his lectures.
If you do not like my answer ask again.
If this website will not produce a suitable answer, maybe the forum at artofproblemsolving.com will (they have Physics sections).
The flow rate in cm%5E3%2Fsecond is
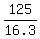125%2F16.3 .
Assuming a perfectly circular cross section, with diameter=0.96cm-->radius=0.48cm ,
the cross section of the stream at the faucet (in cm%5E2 ) is
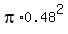
pi%2A0.48%5E2
The linear velocity of the water at the faucet (in cm/second) is
%28%28125%2F16.3%29%29%2F%28pi%2A0.48%5E2%29=about+10.6 .
Under no other force but gravity, that linear velocity would increase with time.
Let t= time in seconds from the moment the water leaves the faucet.
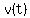v%28t%29= linear velocity of the water (in cm/second) at t seconds.
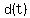d%28t%29= distance between the water and the faucet (in cm) at t seconds.
Let's take the acceleration of gravity as g=9.8m%2Fsecond%5E2=980cm%2Fsecond%5E2 .
Then, v%28t%29=10.6%2B980t and d%28t%29=10.6t%2B980t%5E2%2F2=10.6t%2B490t%5E2
When d%28t%29=13 10.6t%2B490t%5E2=13<--->10.6t%2B490t%5E2-13=0
That quadratic equation would have two solutions, but we are only interested in the positive one.
So we calculate t=%28-10.6+%2B-+sqrt%2810.6%5E2-4%2A490%2A%28-13%29%29%29%2F%282%2A490%29= approximately149.4%2F980=about0.152 seconds.
Then, at that time, water has traveled 13 cm from the faucet and it is moving at a velocity (in cm/s) of
v%280.1542%29=10.6%2B980t=10.6%2B149.4=160
The flow rate cm%5E3%2Fsecond at that point (13 cm from the faucet) is
the same as before, and is equal to
the the linear velocity times the cross section of the stream at that point.
From the flow rate, we could calculate the cross section radius and diameter.
However, it is easier to calculate the diameter knowing that the linear velocity is inversely proportional to the square of the diameter.
The linear velocity increased by a factor of 160%2F10.6=about15.09 ,
so the diameter must have decreased by a factor of sqrt%2810.09%29=about3.9.
So the diameter would be 0.96cm%2F3.9=0.25cm .
The calculation may not quite agree with reality because other physical influences and phenomena may be at work.