A group of 40 workers can finish digging a tunnel in 12 days. how many workers can finish the job in 8 days.
First way: The least common multiple of 12 days and 8 days is 24 days.
>>...A group of 40 workers can finish digging a tunnel in 12 days...<<
Therefore half as many workers (20 workers) could dig it in twice as many
days (24 days).
Therefore it would take 3 times as many workers (60 workers) to dig it
in one-third of 24 days (8 days).
Answer: 60 workers.
Second way:
Use the job-worker-time formula, which is:
where
W1 = the number of workers in the first situation.
T1 = the number of time units (days in this case) in the first situation.
J1 = the number of jobs in the first situation.
W2 = the number of workers in the second situation.
T2 = the number of time units (days in this case) in the second situation.
J2 = the number of jobs in the second situation.
W1 = 40 W2 = the unknown quantity
T1 = 12 T2 = 8
J1 = 1 J2 = 1
[There was only 1 tunnel, so the number of jobs in both situations is 1.
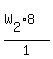480 = 8W2
Divide both sides by 8
60 = W2
Answer: 60 workers.
Edwin
