SOLUTION: During the inter-school competition. rugby and football teams of Orero Boys took part. The probability that the rugby team would win the first match was 3/8while that probability t

Algebra ->  Finance -> SOLUTION: During the inter-school competition. rugby and football teams of Orero Boys took part. The probability that the rugby team would win the first match was 3/8while that probability t      Log On


   

Question 1201930: During the inter-school competition. rugby and football teams of Orero Boys took part. The probability that the rugby team would win the first match was 3/8while that probability that the football team would win the first match was 2/7. Find the probability that at least one the would win the first match.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52790) About Me  (Show Source):
You can put this solution on YOUR website!
.

    P(at least one) = P(one) + P(other) - P(both).


To solve the problem, we need to have the probability P(both), but it is not given in the problem.


So, I made an assumption from OUTSIDE of the problem, that these events are independent;

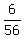then P(both) = %283%2F8%29%2A%282%2F7%29 = 6%2F56.


Then the answer is  

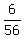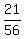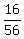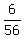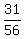    3%2F8 + 2%2F7 - 6%2F56 = 21%2F56 + 16%2F56 - 6%2F56 = 31%2F56 = 0.5536  (rounded).

Solved.



Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


The opposite (complement) of at least one winning is neither winning. So

P(at least one) = 1 - P(neither)

P(neither) = (1-3/8)(1-2/7) = (5/8)(5/7) = 25/56

1-P(neither) = 1-25/56 = 31/56

ANSWER: 31/56

Convert to a decimal or percentage if desired/required....